修改时间:2024-07-12 浏览次数:1254 类型:期末考试
实践探究,解决问题
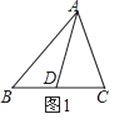
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD .
在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=;

在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为;

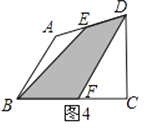
在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.
解决问题:
在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).

试题篮