修改时间:2024-07-12 浏览次数:909 类型:月考试卷
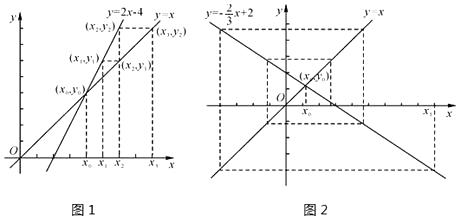
在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k= ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为.
试题篮