河南省2018年中考数学试卷

1. ﹣ $\text{[math]}$ 的相反数是（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . ﹣ $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 今年一季度，河南省对“一带一路”沿线国家进出口总额达214.7亿元，数据“214.7亿”用科学记数法表示为（）

A . 2.147×10² B . 0.2147×10³ C . 2.147×10¹⁰ D . 0.2147×10¹¹

查看解析收藏纠错

+选题
3. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“国”字所在面相对的面上的汉字是（）

A . 厉 B . 害 C . 了 D . 我

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . （﹣x²）³=﹣x⁵ B . x²+x³=x⁵ C . x³•x⁴=x⁷ D . 2x³﹣x³=1

查看解析收藏纠错

+选题
5. 河南省旅游资源丰富，2013～2017年旅游收入不断增长，同比增速分别为：15.3%，12.7%，15.3%，14.5%，17.1%．关于这组数据，下列说法正确的是（）

A . 中位数是12.7% B . 众数是15.3% C . 平均数是15.98% D . 方差是0

查看解析收藏纠错

+选题
6. 《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，还差3钱，问合伙人数、羊价各是多少？设合伙人数为x人，羊价为y钱，根据题意，可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 下列一元二次方程中，有两个不相等实数根的是（）

A . x²+6x+9=0 B . x²=x C . x²+3=2x D . （x﹣1）²+1=0

查看解析收藏纠错

+选题
8. 现有4张卡片，其中3张卡片正面上的图案是“ ”，1张卡片正面上的图案是“ ”，它们除此之外完全相同．把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案相同的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，已知▱AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于 $\text{[math]}$ DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（）

A . （ $\text{[math]}$ ﹣1，2） B . （ $\text{[math]}$ ，2） C . （3﹣ $\text{[math]}$ ，2） D . （ $\text{[math]}$ ﹣2，2）

查看解析收藏纠错

+选题
10. 如图1，点F从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，图2是点F运动时，△FBC的面积y（cm²）随时间x（s）变化的关系图象，则a的值为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 2 $\text{[math]}$

查看解析收藏纠错

+选题

11. 计算：|﹣5|﹣ $\text{[math]}$ =．

查看解析收藏纠错

+选题
12. 如图，直线AB，CD相交于点O，EO⊥AB于点O，∠EOD=50°，则∠BOC的度数为．

查看解析收藏纠错

+选题
13. 不等式组 $\text{[math]}$ 的最小整数解是．

查看解析收藏纠错

+选题
14. 如图，在△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，其中点B的运动路径为 $\text{[math]}$ ，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
15. 如图，∠MAN=90°，点C在边AM上，AC=4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为．

查看解析收藏纠错

+选题

16. 先化简，再求值：（ $\text{[math]}$ ﹣1）÷ $\text{[math]}$ ，其中x= $\text{[math]}$ +1．

查看解析收藏纠错

+选题
17. 每到春夏交替时节，雌性杨树会以满天飞絮的方式来传播下一代，漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等，给人们造成困扰，为了解市民对治理杨絮方法的赞同情况，某课题小组随机调查了部分市民（问卷调查表如表所示），并根据调查结果绘制了如下尚不完整的统计图．
治理杨絮一一您选哪一项？（单选）
A．减少杨树新增面积，控制杨树每年的栽种量
B．调整树种结构，逐渐更换现有杨树
C．选育无絮杨品种，并推广种植
D．对雌性杨树注射生物干扰素，避免产生飞絮
E．其他
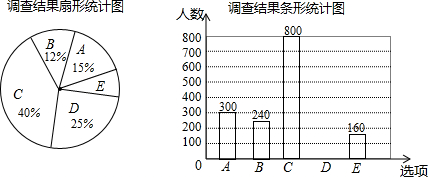
根据以上统计图，解答下列问题：

（1）本次接受调查的市民共有人；

（2）扇形统计图中，扇形E的圆心角度数是；

（3）请补全条形统计图；

（4）若该市约有90万人，请估计赞同“选育无絮杨品种，并推广种植”的人数．

查看解析收藏纠错

+选题
18. 如图，反比例函数y= $\text{[math]}$ （x＞0）的图象过格点（网格线的交点）P．

（1）求反比例函数的解析式；

（2）在图中用直尺和2B铅笔画出两个矩形（不写画法），要求每个矩形均需满足下列两个条件：
①四个顶点均在格点上，且其中两个顶点分别是点O，点P；
②矩形的面积等于k的值．

查看解析收藏纠错

+选题
19. 如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC交DO于点F．

（1）求证：CE=EF；

（2）连接AF并延长，交⊙O于点G．填空：
①当∠D的度数为时，四边形ECFG为菱形；
②当∠D的度数为时，四边形ECOG为正方形．

查看解析收藏纠错

+选题
20. “高低杠”是女子体操特有的一个竞技项目，其比赛器材由高、低两根平行杠及若干支架组成，运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离．某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题，请你解答．
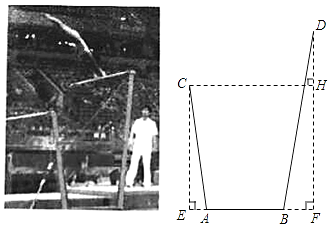
如图所示，底座上A，B两点间的距离为90cm．低杠上点C到直线AB的距离CE的长为155cm，高杠上点D到直线AB的距离DF的长为234cm，已知低杠的支架AC与直线AB的夹角∠CAE为82.4°，高杠的支架BD与直线AB的夹角∠DBF为80.3°．求高、低杠间的水平距离CH的长．（结果精确到1cm，参考数据sin82.4°≈0.991，cos82.4°≈0.132，tan82.4°≈7.500，sin80.3°≈0.983，cos80.3°≈0.168，tan80.3°≈5.850）

查看解析收藏纠错

+选题
21. 某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系关于销售单价，日销售量，日销售利润的几组对应值如表：
销售单价x（元）
85
95
105
115
日销售量y（个）
175
125
75
m
日销售利润w（元）
875
1875
1875
875
（注：日销售利润=日销售量×（销售单价﹣成本单价））

（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；

（2）根据以上信息，填空：
该产品的成本单价是元，当销售单价x=元时，日销售利润w最大，最大值是元；

（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？

查看解析收藏纠错

+选题
22. 如图

（1）问题发现
如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：
① $\text{[math]}$ 的值为；
②∠AMB的度数为．

（2）类比探究
如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断 $\text{[math]}$ 的值及∠AMB的度数，并说明理由；

（3）拓展延伸
在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB= $\text{[math]}$ ，请直接写出当点C与点M重合时AC的长．

查看解析收藏纠错

+选题
23. 如图，抛物线y=ax²+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．

（1）求抛物线的解析式；

（2）过点A的直线交直线BC于点M．
①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；
②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．

查看解析收藏纠错

+选题

河南省2018年中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

销售单价x（元）	85	95	105	115
日销售量y（个）	175	125	75	m
日销售利润w（元）	875	1875	1875	875

河南省2018年中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨