如图，△ABC中，∠ACB=90°，∠B=55°，点D是斜边AB的中点，那么∠ACD的度数为（）

题型：单选题题类：模拟题难易度：容易

北京市昌平区2017年中考数学二模试卷

A、15° B、25° C、35° D、45°

举一反三

如图，已知△ABC≌△ADE ，若∠ABC=70°，∠DAE=80°，则∠C的度数是( )

等腰三角形的周长为20cm，一边长为6cm，则底边长为 {#blank#}1{#/blank#}

在三角形ABC中，∠A=80°，OB、OC分别平分∠ABC和∠ACB，你能求出∠BOC的度数．

二次函数y=ax²+bx+c（a＜0）图象与x轴的交点A、B的横坐标分别为﹣3，1，与y轴交于点C，下面四个结论：

①16a﹣4b+c＜0；②若P（﹣5，y₁），Q（ $\text{[math]}$ ，y₂）是函数图象上的两点，则y₁＞y₂；③a=﹣ $\text{[math]}$ c；④若△ABC是等腰三角形，则b=﹣ $\text{[math]}$ ．其中正确的有{#blank#}1{#/blank#}（请将结论正确的序号全部填上）

如图所示，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F．

认真阅读下面关于三角形内外角平分线的研究片段，完成所提出的问题.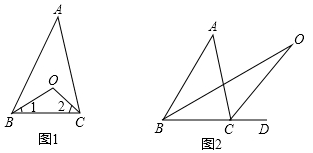

探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+ $\text{[math]}$ ∠A，理由如下：

∵BO和CO分别是∠ABC和∠ACB的角平分线，∴∠1= $\text{[math]}$ ∠ABC，∠2= $\text{[math]}$ ∠ACB．

∴∠1+∠2= $\text{[math]}$ (∠ABC+∠ACB)= $\text{[math]}$ (180°－∠A)=90°－ $\text{[math]}$ ∠A．

∴∠BOC=180°－(∠1+∠2)=180°－(90°－ $\text{[math]}$ ∠A)=90°+ $\text{[math]}$ ∠A

探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.

相关试卷

公司介绍

服务介绍

帮助中心