试题 试卷
题型：单选题 题类：模拟题 难易度：普通
2017年山东省淄博市沂源县中考数学二模试卷
将一副三角板按图中方式叠放，则角α等于（ ）
答案：解答：延长BD交AC于点F，
∵∠BDC是△CDF的外角，∠C=40°，∠BDC=150°，
∴∠CFD=∠BDC-∠C=150°-40°=110°，
∵∠CFD是△ABF的外角，
∴∠BAC+∠ABD=∠CFD=110°，
∵∠ABD，∠BAC的角平分线交于点E，
∴∠BAE+∠ABE= 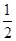（∠BAC+∠ABD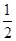）= ×110°=55°，
∴∠AEB=180°-（∠BAE+∠ABE）=180°-55°=125°；
试题篮
B、
C、
D、
（∠BAC+∠ABD）= 
