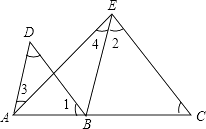
已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D. 解:∵∠1=∠2(已知)
∠1=∠DGH({#blank#}1{#/blank#}),
∴∠2={#blank#}2{#/blank#}( 等量代换 )
∴{#blank#}3{#/blank#}∥{#blank#}4{#/blank#}(同位角相等,两直线平行)
∴∠C={#blank#}5{#/blank#}(两直线平行,同位角相等)
又∵AC∥DF({#blank#}6{#/blank#})
∴∠D=∠ABG ({#blank#}7{#/blank#})
∴∠C=∠D ({#blank#}8{#/blank#})