题型:解答题 题类:真题 难易度:普通
2014年全国高考理数真题试卷(新课标II卷)
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2014 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
附:回归直线的斜率和截距的最小二乘估计公式分别为: =
,
=
﹣
.
|
t |
30 |
40 |
p |
50 |
70 |
|
m |
2 |
4 |
5 |
6 |
8 |
经测算,年广告支出m和年销售额t满足线性回归方程 =6.5m+17.5,则p的值为{#blank#}1{#/blank#}.
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销售量y(件) | 88 | 78 | 85 | 75 | 82 | 66 |
日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
平均气温x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
一天生长的长度y(mm) | 22 | 25 | 29 | 26 | 16 | 12 |
该小组的研究方案是:先从这六组数据中选取6日和11日的两组数据作为检验数据,用剩下的4组数据即:7日至10日的四组数据求出线性回归方程.
| 月份 | | | | | | |
| 广告投入量 | | | | | | |
| 收益 | | | | | | |
他们分别用两种模型① ,②
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
| | | | |
| | | | |
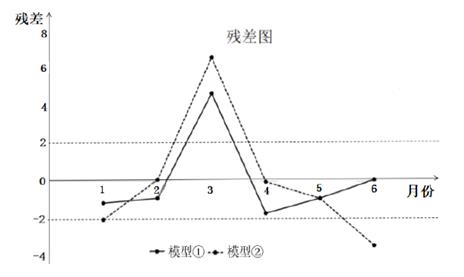
(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于 的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程;
(ⅱ)若广告投入量 时,该模型收益的预报值是多少?
附:对于一组数据 ,
,……,
,其回归直线
的斜率和截距的最小二乘估计分别为:
,
.
试题篮