如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
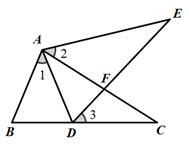
证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC({#blank#}1{#/blank#}),
∴∠2=∠3({#blank#}2{#/blank#}),
又∵∠1=∠3({#blank#}3{#/blank#}),
∴ ∠1=∠2(等量代换),
∴{#blank#}4{#/blank#}+∠DAC= {#blank#}5{#/blank#}+∠DAC({#blank#}6{#/blank#}),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵ 
∴△ABC≌△ADE({#blank#}7{#/blank#}).
