备考2018年数学中考冲刺卷04（深圳专版）

修改时间：2018-05-23 浏览次数：427 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. |-2|的相反数是（）

A . $\text{[math]}$ B . -2 C . $\text{[math]}$ D . 22

查看解析收藏纠错

+选题
2. 如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 李克强总理在2017年政府工作报告中指出：“完善就业政策，加大就业培训力度，加强对灵活就业、新就业形态的支持，今年高校毕业生7950000人，再创历史新高，要实施好就业促进、创业引领、基层成长等计划，促进多渠道就业创业．”其中数据7950000用科学记数法表示是（）

A . 795×10⁴ B . 7.95×10⁵ C . 0.795×10⁷ D . 7.95×10⁶

查看解析收藏纠错

+选题
4. 下列图形中，既是中心对称，又是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 下列说法不正确的是（）

A . 过任意一点可作已知直线的一条平行线 B . 在同一平面内两条不相交的直线是平行线 C . 在同一平面内，过直线外一点只能画一条直线与已知直线垂直 D . 直线外一点与直线上各点连接的所有线段中，垂线段最短

查看解析收藏纠错

+选题
6. 一元一次不等式组 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

查看解析收藏纠错

+选题
7. 某商店有两个进价不同的计算器都卖了64元，其中一个盈利60%，另一个亏损20%，在这次买卖中，这家商店（　　）

A . 不赔不赚 B . 赚了32元 C . 赔了8元 D . 赚了8元

查看解析收藏纠错

+选题
8. 下列作图语句正确的是（　　）

A . 延长线段AB到C，使AB=BC B . 延长射线AB C . 过点A作AB∥CD∥EF D . 作∠AOB的平分线OC

查看解析收藏纠错

+选题
9. 下列四个命题中，真命题有（）
①两条直线被第三条直线所截，内错角相等．
②如果∠1和∠2是对顶角，那么∠1=∠2．
③三角形的一个外角大于任何一个内角．
④如果x²＞0，那么x＞0．

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
10. 在暑假到来之前，某机构向八年级学生推荐了A，B，C三条游学线路，现对全级学生喜欢哪一条游学线路作调查，以决定最终的游学线路，下面的统计量中最值得关注的是（）

A . 方差 B . 平均数 C . 中位数 D . 众数

查看解析收藏纠错

+选题
11. 如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B，C两地相距120海里．若“中海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离．（）

A . 40 $\text{[math]}$ B . 60﹣20 $\text{[math]}$ C . 20 $\text{[math]}$ D . 20

查看解析收藏纠错

+选题
12. 如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC，DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论中结论正确的有（）
①EG=DF；
②∠AEH+∠ADH=180°；
③△EHF≌△DHC；
④若 $\text{[math]}$ = $\text{[math]}$ ，则S_△_EDH=13S_△_CFH ．

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题

二、填空题

13. 分解因式：5x³﹣10x²+5x=．

查看解析收藏纠错

+选题
14. 甲、乙、丙三人玩“丢飞碟”游戏，飞碟从一人传到另一人记为丢一次，若从乙开始，则丢两次后，飞碟传到丙处的概率为．

查看解析收藏纠错

+选题
15. 已知a+b=3，ab=2，则a²+b²的值为．

查看解析收藏纠错

+选题
16. 如图，已知在正方形ABCD中，F是CD边上一点（不和C，D重合），过点D做DG⊥BF交BF延长线于点G．连接AG，交BD于点E，连接EF，交CD于点M．若DG=6，AG=7 $\text{[math]}$ ，则EF的长为．

查看解析收藏纠错

+选题

三、解答题

17. 计算：|2﹣tan60°|﹣（π﹣3.14）⁰+（- $\text{[math]}$ ）^﹣2+ $\text{[math]}$ $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 先化简，再求值：（ $\text{[math]}$ +2﹣x）÷ $\text{[math]}$ ，其中x满足x²+2x﹣3=0．

查看解析收藏纠错

+选题
19. 在“爱满扬州”慈善一日捐活动中，学校团总支为了了解本校学生的捐款情况，随机抽取了50名学生的捐款数进行了统计，并绘制成统计图．

（1）这50名同学捐款的众数为元，中位数为元；

（2）求这50名同学捐款的平均数；

（3）该校共有600名学生参与捐款，请估计该校学生的捐款总数．

查看解析收藏纠错

+选题
20.
已知：如图，在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，点P从点B出发，沿BC向点C匀速运动，速度为1cm/s；过点P作PD∥AB，交AC于点D，同时，点Q从点A出发，沿AB向点B匀速运动，速度为2cm/s；当一个点停止运动时，另一个点也停止运动，连接PQ．设运动时间为t（s）（0＜t＜2.5），解答下列问题：

（1）当t为何值时，四边形ADPQ为平行四边形？

（2）设四边形ADPQ的面积为y（cm²），试确定y与t的函数关系式；

（3）在运动过程中，是否存在某一时刻t，使S_四边形_ADPQ：S_△_PQB=13：2？若存在，请说明理由，若存在，求出t的值，并求出此时PQ的距离．

查看解析收藏纠错

+选题
21. 如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数y= $\text{[math]}$ 的图象在第二象限交于点C，CE⊥x轴，垂足为点E，tan∠ABO= $\text{[math]}$ ，OB=4，OE=2．

（1）求反比例函数的解析式；

（2）若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF．如果S_△_BAF=4S_△_DFO ，求点D的坐标．

查看解析收藏纠错

+选题
22.
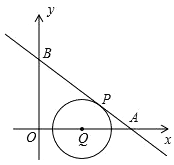
如图在平面直角坐标系中，直线y=﹣ $\text{[math]}$ x+3与x轴、y轴分别交于A、B两点，点P、Q同时从点A出发，运动时间为t秒．其中点P沿射线AB运动，速度为每秒4个单位长度，点Q沿射线AO运动，速度为每秒5个单位长度．以点Q为圆心，PQ长为半径作⊙Q．

（1）求证：直线AB是⊙Q的切线；

（2）过点A左侧x轴上的任意一点C（m，0），作直线AB的垂线CM，垂足为M．若CM与⊙Q相切于点D，求m与t的函数关系式（不需写出自变量的取值范围）；

（3）在（2）的条件下，是否存在点C，直线AB、CM、y轴与⊙Q同时相切？若存在，请直接写出此时点C的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
23.
矩形AOCD绕顶点A（0，5）逆时针方向旋转，当旋转到如图所示的位置时，边BE交边CD于M，且ME=2，CM=4．

（1）求AD的长；

（2）求阴影部分的面积和直线AM的解析式；

（3）求经过A、B、D三点的抛物线的解析式；

（4）在抛物线上是否存在点P，使S_△_PAM= $\text{[math]}$ ？若存在，求出P点坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

备考2018年数学中考冲刺卷04（深圳专版）

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨