【培优卷】3.9弧长及扇形的面积—2023-2024学年北师大版九年级下册同步测试

1. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的一个动点，连结 $\text{[math]}$ ，点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，当 $\text{[math]}$ 运动时， $\text{[math]}$ 也随之运动．若 $\text{[math]}$ 从 $\text{[math]}$ 运动到 $\text{[math]}$ ，则点 $\text{[math]}$ 经过的路径长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 已知点A，B，C在⊙O上，∠ABC=30°，把劣弧 $\text{[math]}$ 沿着直线CB折叠交弦AB于点D．若BD=9，AD=6，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ π B . 3π C . $\text{[math]}$ π D . $\text{[math]}$ π

查看解析收藏纠错

+选题
3. 已知在扇形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为弧 $\text{[math]}$ 的中点， $\text{[math]}$ 为半径 $\text{[math]}$ 上一动点，点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，若点 $\text{[math]}$ 落在扇形 $\text{[math]}$ 内 $\text{[math]}$ 不含边界 $\text{[math]}$ ，则 $\text{[math]}$ 长的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是边 $\text{[math]}$ 、 $\text{[math]}$ 的中点，某一时刻，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向以每秒2个单位长度的速度向点 $\text{[math]}$ 匀速运动；同时，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向以每秒1个单位长度的速度向点 $\text{[math]}$ 匀速运动，其中一点运动到矩形顶点时，两点同时停止运动，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ .在这一运动过程中，点 $\text{[math]}$ 所经过的路径长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接正方形，直线 $\text{[math]}$ 且平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ ，则阴影部分面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，在边长为4的正六边形 $\text{[math]}$ 中，先以点B为圆心， $\text{[math]}$ 的长为半径作 $\text{[math]}$ ，再以点A为圆心， $\text{[math]}$ 的长为半径作 $\text{[math]}$ 交 $\text{[math]}$ 于点P，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， BO＝2cm，将 $\text{[math]}$ 绕点O逆时针旋转至 $\text{[math]}$ ，点 $\text{[math]}$ 在BO的延长线上，则边BC扫过区域（图中阴影部分）的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，正方形ABCD的边长是 $\text{[math]}$ ，以正方形对角线的一半OA为边作正六边形，其中一边与正方形的边CD交于点E，再以点O为圆心OE为半径画弧交AD于点F，则图中阴影部分的的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

9. 如图，正六边形 $\text{[math]}$ 的边长为2，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径画弧，得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
10. 如图，在菱形ABCD中，点E是AB的中点，以B为圆心，BE为半径作弧，交BC于F，连接DE、DF．若AB=2，∠A=60°，则阴影部分的面积为

查看解析收藏纠错

+选题
11. 如图，已知 $\text{[math]}$ 是△ABC的外接圆，且圆心O在线段AB上，点D是 $\text{[math]}$ 上一点，DA的延长线与过点C的切线交于点E，且 $\text{[math]}$ ，连接CD交AB于点F，①若 $\text{[math]}$ ， $\text{[math]}$ 的半径 $\text{[math]}$ ，则 $\text{[math]}$ ；②若 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
12. 如图，四边形ABCD是边长为 $\text{[math]}$ 的正方形，曲线DA₁B₁C₁D₁A₂ …是由多段90°的圆心角所对的弧组成的.其中，弧DA₁的圆心为A，半径为AD；弧A₁B₁的圆心为B，半径为BA₁；弧B₁C₁的圆心为C，半径为CB₁；弧C₁D₁的圆心为D，半径为DC₁….弧DA₁、弧A₁B₁、弧B₁C₁、弧C₁D₁…的圆心依次按点A，B，C，D循环，则弧C₂₀₂₂D₂₀₂₂的长是（结果保留π）.

查看解析收藏纠错

+选题

13. 如图①，在Rt△ABC中，∠C=90°，∠A=60°，AC=3cm，边AB在直线l上．将Rt△ABC沿直线l作无滑动翻滚，当Rt△ABC翻滚一周时，求点A经过的路径长要解决这个问题，先要弄清在翻滚时点A经过的路径是什么Rt△ABC翻滚一周即为翻滚三次，第一次翻滚点A经过的路径长是以点B为圆心、AB为半径、圆心角是150°的 $\text{[math]}$ 的长，即为5πcm；第二次翻滚点A经过的路线长是以点C1为圆心、A₁C₁为半径圆心角是90°的 $\text{[math]}$ 的长，即为 $\text{[math]}$ πcm；第三次翻滚时点A没动．所以Rt△ABC翻滚一周点A经过的路径是5π+ $\text{[math]}$ π= $\text{[math]}$ π(cm)．
思考：如图②，在矩形ABCD中，AB=4，BC=3，边CD在直线l上．将矩形ABCD沿直线l作无滑动翻滚，当点A第一次翻滚到点A1位置时，求点A经过的路径长．

查看解析收藏纠错

+选题
14. 小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数 $\text{[math]}$ 图象上的点 $\text{[math]}$ 和点B为顶点，分别作菱形AOCD和菱形OBEF，点D，E在x轴上，以点O为圆心，OA长为半径作 $\text{[math]}$ ，连接BF．

（1）求k的值；

（2）求扇形AOC的半径及圆心角的度数；

（3）请直接写出图中阴影部分面积之和．

查看解析收藏纠错

+选题
15. 项目化学习：车轮的形状．
【问题提出】车轮为什么要做成圆形，这里面有什么数学原理?

（1）
【合作探究】

探究 $\text{[math]}$ 组：如图1，圆形车轮半径为 $\text{[math]}$ ，其车轮轴心 $\text{[math]}$ 到地面的距离始终为 $\text{[math]}$ ．
探究 $\text{[math]}$ 组：如图2，正方形车轮的轴心为 $\text{[math]}$ ，若正方形的边长为 $\text{[math]}$ ，求车轮轴心 $\text{[math]}$ 最高点与最低点的高度差．
探究 $\text{[math]}$ 组：如图3，有一个破损的圆形车轮，半径为 $\text{[math]}$ ，破损部分是一个弓形，其所对圆心角为 $\text{[math]}$ ，其车轮轴心为 $\text{[math]}$ ，让车轮在地上无滑动地滚动一周，求点 $\text{[math]}$ 经过的路程．

探究发现：车辆的平稳关键看车轮轴心是否稳定．

（2）
【拓展延伸】如图4，分别以正三角形的三个顶点 $\text{[math]}$ 为圆心，以正三角形的边长为半径作 $\text{[math]}$ 圆弧，这个曲线图形叫做“莱洛三角形”．

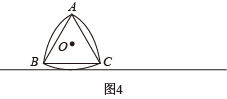
探究 $\text{[math]}$ 组：使 “莱洛三角形” 沿水平方向向右滚动，在滚动过程中，其每时每刻都有 “最高点”，“中心点” 也在不断移动位置，那么在 “莱洛三角形” 滚动一周的过程中，其“最高点”和“中心点”所形成的图案大致是．
延伸发现：“莱洛三角形”在滚动时始终位于一组平行线之间，因此放在其上的物体也能够保持平衡，但其车轴中心 $\text{[math]}$ 并不稳定．

查看解析收藏纠错

+选题

【培优卷】3.9弧长及扇形的面积—2023-2024学年北师大版九年级下册同步测试

一、选择题

二、填空题

三、解答题

相关试卷收起∨

【培优卷】3.9弧长及扇形的面积—2023-2024学年北师大版九年级下册同步测试

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨