修改时间:2023-10-16 浏览次数:122 类型:单元试卷

其中,校验码是用来校验商品条形码中前12位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:
步骤1:计算前12位数字中偶数位数字的和
,即
;
步骤2:计算前12位数字中奇数位数字的和
,即
;
步骤3:计算
与
的和
,即
;
步骤4:取大于或等于
且为10的整数倍的最小数
,即中
;
步骤5:计算
与
的差就是校验码X,即
.
如图,若条形码中被污染的两个数字的和是5,则被污染的两个数字中右边的数字是.
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 | 0.90 | |
超过17吨但不超过30吨的部分 | 0.90 | |
超过30吨的部分 | 6.00 | 0.90 |
说明:每户生产的污水量等于该户自来水用量;
水费
自来水费用
污水处理费
已知小王家2018年7月用水16吨,交水费43.2元.8月份用水25吨,交水费75.5元.
|
商场 |
优惠活动 |
|
甲 |
全场按标价的6折销售 |
|
乙 |
实行“每满100元送100元的购物券”的优惠,购物券可以在再购买时冲抵现金比如:顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券) |
|
丙 |
实行“每满100元减50元的优惠”(比如,某顾客购物220元,他只需付款120元) |
根据以上活动信息,解决以下问题:
若、
、
为数轴上三点,若点
到
的距离是点
到
的距离
倍,我们就称点
是【
,
】的好点.
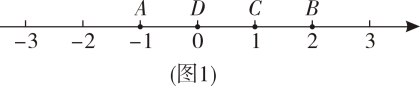
例如,如图 , 点
表示的数为
, 点
表示的数为
表示
的点
到点
的距离是
, 到点
的距离是
, 那么点
是【
,
】的好点;又如,表示
的点
到点
的距离是
, 到点
的距离是
, 那么点
就不是【
,
】的好点,但点
是【
,
】的好点.
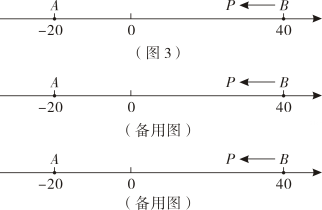
知识运用:如图 ,
、
为数轴上两点,点
所表示的数为
, 点
所表示的数为
.

试题篮