浙教版备考2023年中考数学一轮复习55.勾股定理及其应用

修改时间：2023-01-03 浏览次数：166 类型：一轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题（每题3分，共30分）

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， D是AB的中点，延长CB至点E，使 $\text{[math]}$ ，连接DE，F为DE中点，连接BF.若 $\text{[math]}$ ， $\text{[math]}$ ，则BF的长为（）

A . 5 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题
2. 如图，三角形纸片ABC中，∠BAC＝90°，AB＝2，AC＝3．沿过点A的直线将纸片折叠，使点B落在边BC上的点D处；再折叠纸片，使点C与点D重合，若折痕与AC的交点为E，则AE的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，在Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点B顺时针旋转90°得到 $\text{[math]}$ .在此旋转过程中 $\text{[math]}$ 所扫过的面积为（）

A . 25π+24 B . 5π+24 C . 25π D . 5π

查看解析收藏纠错

+选题
4. 如图，在正方形方格纸中，每个小正方形的边长都相等，A，B，C，D都在格点处，AB与CD相交于点P，则cos∠APC的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，正方形 $\text{[math]}$ 的对角线交于点O，点E是直线 $\text{[math]}$ 上一动点．若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图是两个全等的直角三角形拼成的图形，且点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上，连结 $\text{[math]}$ 设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积可以表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，正方形ABCD边长为1，以AC为边作第2个正方形ACEF，再以CF为边作第3个正方形FCGH，…，按照这样的规律作下去，第6个正方形的边长为（）

A . （2 $\text{[math]}$ ）⁵ B . （2 $\text{[math]}$ ）⁶ C . （ $\text{[math]}$ ）⁵ D . （ $\text{[math]}$ ）⁶

查看解析收藏纠错

+选题
8. 有一直角三角形纸片，∠C＝90°BC＝6，AC＝8，现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则CE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
9. 我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭（jiǎ）生其中，出水一尺，引葭赴岸，适与岸齐.间水深几何.”（丈、尺是长度单位，1丈 $\text{[math]}$ 尺，）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度是多少？则水深为（）

A . 10尺 B . 11尺 C . 12尺 D . 13尺

查看解析收藏纠错

+选题
10. 数形结合是数学的重要思想和解题方法，如：“当0＜x＜12时，求代数式 $\text{[math]}$ 的最小值”，其中 $\text{[math]}$ 可看作两直角边分别为x和2的Rt△ACP的斜边长， $\text{[math]}$ 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值，如图所示，当AP与BP共线时，AP+BP为最小.请你解决问题：当0＜x＜4时，则代数式 $\text{[math]}$ 的最小值是（）

A . 4 B . 5 C . 6 D . 7

查看解析收藏纠错

+选题

二、填空题（每题3分，共18分）

11. 如图，将矩形纸片ABCD沿CE折叠，使点B落在边AD上的点F处．若点E在边AB上，AB＝3，BC＝5，则AE＝．

查看解析收藏纠错

+选题
12. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上除 $\text{[math]}$ ， $\text{[math]}$ 点外的任意一点，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
13. 沐沐用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的对角线长为．

查看解析收藏纠错

+选题
14. 如图所示的象棋盘中，各个小正方形的边长均为1.“马”从图中的位置出发，不走重复路线，按照“马走日”的规则，走两步后的落点与出发点间的最短距离为.

查看解析收藏纠错

+选题
15. 我国古代数学家赵爽创制了一幅“赵爽弦图”，极富创新意识地给出了勾股定理的证明.如图所示，“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，若大正方形的面积是25，小正方形的面积是1，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
16. 勾股定理最早出现在商高的《周髀算经》：“勾广三，股修四，经隅五”.观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1，柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为2m（m≥3，m为正整数），则其弦是（结果用含m的式子表示）.

查看解析收藏纠错

+选题

三、解答题（共8题，共72分）

17. 在 $\text{[math]}$ 的网格中，设每一个小方格的边长为1个单位，画出4个不同的正方形 $\text{[math]}$ 用阴影部分表示 $\text{[math]}$ ，所画正方形的顶点都在方格的顶点上，且面积均小于9，并写出相应正方形的边长.

查看解析收藏纠错

+选题
18. 如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13米，此人以0.5米/秒的速度收绳，10秒后船移动到点D的位置，问船向岸边移动了多少米？(假设绳子是直的，结果保留根号)

查看解析收藏纠错

+选题
19. 已知 $\text{[math]}$ 的三条边长分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 是直角三角形吗？请证明你的判断.

查看解析收藏纠错

+选题

20. 阅读与应用：

下面是小敏学习实数之后，写的数学日记的一部分，请你认真阅读，并完成相应的任务．

2022年9月22日天气：晴

无理数与线段长．今天我们借助勾股定理，在数轴上找到了一些特殊的无理数对应的点，认识了“数轴上的点与实数一一对应”这一事实．

回顾梳理：要在数轴上找到表示 $\text{[math]}$ 的点，关键是在数轴上构造线段 $\text{[math]}$ ．如图1，正方形的边长为1个单位长度，以原点O为圆心，对角线长为半径画弧与数轴分别交于点A， $\text{[math]}$ ，则点A对应的数为 $\text{[math]}$ ，点 $\text{[math]}$ 对应的数为 $\text{[math]}$ ．类似地，我们可以在数轴上找到表示 $\text{[math]}$ ， $\text{[math]}$ ， …的点．

拓展思考：如图2，改变图1中正方形的位置，用类似的方法作图，可在数轴上构造出线段 $\text{[math]}$ 与 $\text{[math]}$ ，其中O仍为原点，点B， $\text{[math]}$ 分别在原点的右侧、左侧，可由线段 $\text{[math]}$ 与 $\text{[math]}$ 的长得到点B， $\text{[math]}$ 所表示的无理数！

按照这样的思路，只要构造出特定长度的线段，就能在数轴上找到无理数对应的点！

任务：

（1） “拓展思考”中，线段 $\text{[math]}$ 的长为， $\text{[math]}$ 的长为；点B表示的数为，点 $\text{[math]}$ 表示的数为．

（2）请从A，B两题中任选一题作答．我选择题．

A．请在图3所示的数轴上，画图确定表示 $\text{[math]}$ 的点M，N；

B．请在图3所示的数轴上，画图确定表示 $\text{[math]}$ 的点M．

查看解析收藏纠错

+选题

21. 综合与实践

（1）知识再现
如图 $\text{[math]}$ ， $\text{[math]}$ 中， $\text{[math]}$ ，分别以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为边向外作的正方形的面积为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．当 $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ ．

（2）问题探究

如图， $\text{[math]}$ 中， $\text{[math]}$ ．
如图 $\text{[math]}$ ，分别以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为边向外作的等腰直角三角形的面积为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系是．

（3）如图 $\text{[math]}$ ，分别以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为边向外作的等边三角形的面积为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，试猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由．

（4）实践应用
如图4，将图 $\text{[math]}$ 中的 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转一定角度至 $\text{[math]}$ ， $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转一定角度至 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ．求证： $\text{[math]}$ ；

（5）如图5，分别以图 $\text{[math]}$ 中 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为直径向外作半圆，再以所得图形为底面作柱体， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为直径的半圆柱的体积分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．若 $\text{[math]}$ ，柱体的高 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
22. 【经典回顾】
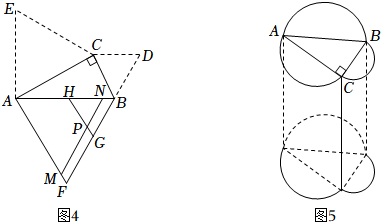
梅文鼎是我国清初著名的数学家，他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线．

在 $\text{[math]}$ 中， $\text{[math]}$ ，四边形 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ 分别是以 $\text{[math]}$ 的三边为一边的正方形．延长 $\text{[math]}$ 和 $\text{[math]}$ ，交于点 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．

（1）证明： $\text{[math]}$ ；

（2）证明：正方形 $\text{[math]}$ 的面积等于四边形 $\text{[math]}$ 的面积；

（3）请利用（2）中的结论证明勾股定理．

（4）【迁移拓展】
如图2，四边形 $\text{[math]}$ 和 $\text{[math]}$ 分别是以 $\text{[math]}$ 的两边为一边的平行四边形，探索在 $\text{[math]}$ 下方是否存在平行四边形 $\text{[math]}$ ，使得该平行四边形的面积等于平行四边形 $\text{[math]}$ 、 $\text{[math]}$ 的面积之和．若存在，作出满足条件的平行四边形 $\text{[math]}$ （保留适当的作图痕迹）；若不存在，请说明理由．

查看解析收藏纠错

+选题
23. 综合与实践

（1）问题情境：在Rt△ABC中，∠BAC=90°，AB=6，AC=8．直角三角板EDF中∠EDF=90°，将三角板的直角顶点D放在Rt△ABC斜边BC的中点处，并将三角板绕点D旋转，三角板的两边DE，DF分别与边AB，AC交于点M，N，猜想证明：
如图①，在三角板旋转过程中，当点M为边AB的中点时，试判断四边形AMDN的形状，并说明理由；

（2）问题解决：
如图②，在三角板旋转过程中，当 $\text{[math]}$ 时，求线段CN的长；

（3）如图③，在三角板旋转过程中，当AM=AN时，直接写出线段AN的长．

查看解析收藏纠错

+选题
24. 将矩形纸片 $\text{[math]}$ 放在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ ．现绕点O顺时针旋转矩形纸片 $\text{[math]}$ ，得到新的矩形 $\text{[math]}$ ，其中A，B，C的对应点分别为 $\text{[math]}$ ．当直线 $\text{[math]}$ 与直线 $\text{[math]}$ 有交点时，设交点为D．

（1）在旋转过程中，判断线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并以图①为例说明理由；

（2）在旋转过程中，当点 $\text{[math]}$ 落在线段 $\text{[math]}$ 上时（如图②），直接写出点 $\text{[math]}$ 的坐标；

（3）在旋转过程中，若线段 $\text{[math]}$ 恰好过线段 $\text{[math]}$ 中点E时（如图③），求线段 $\text{[math]}$ 的长；

（4）在旋转过程中，当线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的交点M恰好是线段 $\text{[math]}$ 中点时（如图④），请直接写出点M和点D的坐标．

查看解析收藏纠错

+选题

浙教版备考2023年中考数学一轮复习55.勾股定理及其应用

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

相关试卷 收起∨

相关试卷收起∨