四川省达州市2020年中考数学试卷

1. 人类与病毒的斗争是长期的，不能松懈．据中央电视台“朝日新闻”报道，截止北京时间2020年6月30日凌晨，全球新冠肺炎患者确诊病例达到1002万.1002万用科学记数法表示，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 万

查看解析收藏纠错

+选题
2. 下列各数中，比3大比4小的无理数是（）

A . 3.14 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列正方体的展开图上每个面上都有一个汉字．其中，手的对面是口的是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列说法正确的是（）

A . 为了解全国中小学生的心理健康状况，应采用普查． B . 确定事件一定会发生． C . 某校6位同学在新冠肺炎防疫知识竞赛中成绩分别为98、97、99、99、98、96，那么这组数据的众数为98． D . 数据6、5、8、7、2的中位数是6．

查看解析收藏纠错

+选题
5. 图2是图1中长方体的三视图，若用S表示面积， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，正方体的每条棱上放置相同数目的小球，设每条棱上的小球数为m，下列代数式表示正方体上小球总数，则表达错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 中国奇书《易经》中记载，远古时期，人们通过在绳子上打结来计数，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满5进1，用来记录孩子自出生后的天数．由图可知，孩子自出生后的天数是（）

A . 10 B . 89 C . 165 D . 294

查看解析收藏纠错

+选题
8. 如图，在半径为5的 $\text{[math]}$ 中，将劣弧 $\text{[math]}$ 沿弦 $\text{[math]}$ 翻折，使折叠后的 $\text{[math]}$ 恰好与 $\text{[math]}$ 、 $\text{[math]}$ 相切，则劣弧AB的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 交于A、B两点，则 $\text{[math]}$ 的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
10. 如图， $\text{[math]}$ ， $\text{[math]}$ ，点A在 $\text{[math]}$ 上，四边形 $\text{[math]}$ 是矩形，连接 $\text{[math]}$ 、 $\text{[math]}$ 交于点E，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点F．下列4个判断：① $\text{[math]}$ 平分 $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若点G是线段 $\text{[math]}$ 的中点，则 $\text{[math]}$ 为等腰直角三角形．正确判断的个数是（）

A . 4 B . 3 C . 2 D . 1

查看解析收藏纠错

+选题

11. 2019年是中华人民共和国成立70周年，天安门广场举行了盛大的国庆阅兵式和群众游行活动．其中，群众游行队伍以“同心共筑中国梦”为主题，包含有“建国创业”“改革开放”“伟大复兴”三个部分，某同学要统计本班学生最喜欢哪个部分，制作扇形统计图．以下是打乱了的统计步骤：
①绘制扇形统计图

②收集三个部分本班学生喜欢的人数

③计算扇形统计图中三个部分所占的百分比

其中正确的统计顺序是．

查看解析收藏纠错

+选题
12. 如图，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
13. 小明为测量校园里一颗大树 $\text{[math]}$ 的高度，在树底部B所在的水平面内，将测角仪 $\text{[math]}$ 竖直放在与B相距 $\text{[math]}$ 的位置，在D处测得树顶A的仰角为 $\text{[math]}$ ．若测角仪的高度是 $\text{[math]}$ ，则大树 $\text{[math]}$ 的高度约为．（结果精确到 $\text{[math]}$ ．参考数据： $\text{[math]}$ ）

查看解析收藏纠错

+选题
14. 如图，点A、B在反比函数 $\text{[math]}$ 的图象上，A、B的纵坐标分别是3和6，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 的面积是．

查看解析收藏纠错

+选题
15. 已知 $\text{[math]}$ 的三边a、b、c满足 $\text{[math]}$ ，则 $\text{[math]}$ 的内切圆半径=．

查看解析收藏纠错

+选题
16. 已知k为正整数，无论k取何值，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 都交于一个固定的点，这个点的坐标是；记直线 $\text{[math]}$ 和 $\text{[math]}$ 与x轴围成的三角形面积为 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题

17. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 求代数式 $\text{[math]}$ 的值，其中 $\text{[math]}$ ．

查看解析收藏纠错

+选题
19. 如图，点O在 $\text{[math]}$ 的边 $\text{[math]}$ 上，以 $\text{[math]}$ 为半径作 $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点D，过点D作 $\text{[math]}$ 于点E．

（1）尺规作图（不写作法，保留作图痕迹），补全图形；

（2）判断 $\text{[math]}$ 与 $\text{[math]}$ 交点的个数，并说明理由．

查看解析收藏纠错

+选题
20. 争创全国文明城市，从我做起．尚理中学在八年级开设了文明礼仪校本课程，为了解学生的学习情况，随机抽取了20名学生的测试成绩，分数如下：
94 83 90 86 94 88 96 100 89 82

94 82 84 89 88 93 98 94 93 92

整理上面的数据，得到频数分布表和扇形统计图：

等级

成绩/分

频数

A

$\text{[math]}$

a

B

$\text{[math]}$

8

C

$\text{[math]}$

5

D

$\text{[math]}$

4

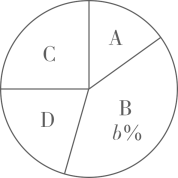
根据以上信息，解答下列问题．

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ；

（2）若成绩不低于90分为优秀，估计该校1200名八年级学生中，达到优秀等级的人数；

（3）已知A等级中有2名女生，现从A等级中随机抽取2名同学，试用列表或画树状图的方法求出恰好抽到一男一女的概率．

查看解析收藏纠错

+选题
21. 如图， $\text{[math]}$ 中， $\text{[math]}$ ，D、E分别是边 $\text{[math]}$ 、 $\text{[math]}$ 的中点．将 $\text{[math]}$ 绕点E旋转180度，得 $\text{[math]}$ ．

（1）判断四边形 $\text{[math]}$ 的形状，并证明；

（2）已知 $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积S．

查看解析收藏纠错

+选题

22. 某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：

	原进价（元/张）	零售价（元/张）	成套售价（元/套）
餐桌	a	380	940
餐椅	$\text{[math]}$	160	940

已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同．

（1）求表中a的值；

（2）该商场计划购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．若将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售，请问怎样进货，才能获得最大利润？最大利润是多少？

查看解析收藏纠错

+选题

23. 如图，在梯形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．P为线段 $\text{[math]}$ 上的一动点，且和B、C不重合，连接 $\text{[math]}$ ，过点P作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点E．

聪聪根据学习函数的经验，对这个问题进行了研究：

（1）通过推理，他发现 $\text{[math]}$ ，请你帮他完成证明．

（2）利用几何画板，他改变 $\text{[math]}$ 的长度，运动点P，得到不同位置时， $\text{[math]}$ 、 $\text{[math]}$ 的长度的对应值：

当 $\text{[math]}$ 时，得表1：

$\text{[math]}$	…	1	2	3	4	5	…
$\text{[math]}$	…	0.83	1.33	1.50	1.33	0.83	…

当 $\text{[math]}$ 时，得表2：

$\text{[math]}$	…	1	2	3	4	5	6	7	…
$\text{[math]}$	…	1.17	2.00	2.50	2.67	2.50	2.00	1.17	…

这说明，点P在线段 $\text{[math]}$ 上运动时，要保证点E总在线段 $\text{[math]}$ 上， $\text{[math]}$ 的长度应有一定的限制．

①填空：根据函数的定义，我们可以确定，在 $\text{[math]}$ 和 $\text{[math]}$ 的长度这两个变量中，的长度为自变量，的长度为因变量；

②设 $\text{[math]}$ ，当点P在线段 $\text{[math]}$ 上运动时，点E总在线段 $\text{[math]}$ 上，求m的取值范围．

查看解析收藏纠错

+选题

24.

（1）（阅读与证明）
如图1，在正 $\text{[math]}$ 的外角 $\text{[math]}$ 内引射线 $\text{[math]}$ ，作点C关于 $\text{[math]}$ 的对称点E（点E在 $\text{[math]}$ 内），连接 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 于点F、G．

①完成证明： $\text{[math]}$ 点E是点C关于 $\text{[math]}$ 的对称点，

$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

$\text{[math]}$ 正 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，

$\text{[math]}$ ，得 $\text{[math]}$ ．

在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．

在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．

②求证： $\text{[math]}$ ．

（2）（类比与探究）
把（1）中的“正 $\text{[math]}$ ”改为“正方形 $\text{[math]}$ ”，其余条件不变，如图2．类比探究，可得：

① $\text{[math]}$ $\text{[math]}$ ；

②线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间存在数量关系．

（3）（归纳与拓展）
如图3，点A在射线 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ，在 $\text{[math]}$ 内引射线 $\text{[math]}$ ，作点C关于 $\text{[math]}$ 的对称点E（点E在 $\text{[math]}$ 内），连接 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 于点F、G．则线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系为．

查看解析收藏纠错

+选题
25. 如图，在平面直角坐标系 xOy 中，已知直线 $\text{[math]}$ 与x轴交于点A，与y轴交于点B，过A、B两点的抛物线 $\text{[math]}$ 与x轴交于另一点 $\text{[math]}$ ．

（1）求抛物线的解析式；

（2）在抛物线上是否存在一点P，使 $\text{[math]}$ ？若存在，请求出点P的坐标，若不存在，请说明理由；

（3）点M为直线 $\text{[math]}$ 下方抛物线上一点，点N为y轴上一点，当 $\text{[math]}$ 的面积最大时，求 $\text{[math]}$ 的最小值．

查看解析收藏纠错

+选题

四川省达州市2020年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

等级	成绩/分	频数
A	$\text{[math]}$	a
B	$\text{[math]}$	8
C	$\text{[math]}$	5
D	$\text{[math]}$	4

四川省达州市2020年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨