江苏省徐州巿2018年中考数学试卷

1. 4的平方根是（）

A . $\text{[math]}$ B . 2 C . －2 D . 16

查看解析收藏纠错

+选题
2. 一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为（）

A . 11.18×10³万元 B . 1.118×10⁴万元 C . 1.118×10⁵万元 D . 1.118×10⁸万元

查看解析收藏纠错

+选题
3. 函数 $\text{[math]}$ 中自变量x的取值范围是（）

A . x≥－1 B . x≤－1 C . x≠－1 D . x＝－1

查看解析收藏纠错

+选题
4. 下列运算中，正确的是（）

A . x³+x³=x⁶ B . x³·x⁹=x²⁷ C . (x²)³=x⁵ D . x $\text{[math]}$ x²=x^－1

查看解析收藏纠错

+选题
5. 如果点（3，－4）在反比例函数 $\text{[math]}$ 的图象上，那么下列各点中，在此图象上的是（）

A . （3，4） B . （－2，－6） C . （－2，6） D . （－3，－4）

查看解析收藏纠错

+选题
6. 下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能折成无盖小方盒的是（）

A . B . C . D .

查看解析收藏纠错

+选题
7. ⊙O₁和⊙O₂的半径分别为5和2，O₁O₂＝3，则⊙O₁和⊙O₂的位置关系是（）

A . 内含 B . 内切 C . 相交 D . 外切

查看解析收藏纠错

+选题
8. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A . 正三角形 B . 菱形 C . 直角梯形 D . 正六边形

查看解析收藏纠错

+选题
9. 下列事件中，必然事件是（）

A . 抛掷1个均匀的骰子，出现6点向上 B . 两直线被第三条直线所截，同位角 C . 366人中至少有2人的生日相同 D . 实数的绝对值是非负数

查看解析收藏纠错

+选题
10. 如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 因式分解：2x²-8=

查看解析收藏纠错

+选题
12. 徐州巿部分医保定点医院2018年第一季度的人均住院费用（单位：元）约为：12 320，11 880，10 370，8 570，10 640， 10240.这组数据的极差是元.

查看解析收藏纠错

+选题
13. 若 $\text{[math]}$ 为方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 边长为a的正三角形的面积等于.

查看解析收藏纠错

+选题
15. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D.若，若∠C＝18°，则∠CDA＝.

查看解析收藏纠错

+选题
16. 如图，Rt△ABC中，∠B＝90°，AB＝3cm，AC＝5cm，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于cm.

查看解析收藏纠错

+选题

17. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 已知 $\text{[math]}$

查看解析收藏纠错

+选题
19. 解不等式组 $\text{[math]}$ ，并写出它的所有整数解.

查看解析收藏纠错

+选题
20. 如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m）参考数据： $\text{[math]}$ $\text{[math]}$ 1.414， $\text{[math]}$ $\text{[math]}$ 1.732

查看解析收藏纠错

+选题

21. （A类）已知如图，四边形ABCD中，AB＝BC，AD＝CD，求证：∠A＝∠ C.
（B类）已知如图，四边形ABCD中，AB＝BC，∠A＝∠C，求证：AD＝CD.

查看解析收藏纠错

+选题

22. 从称许到南京可乘列车A与列车B，已知徐州至南京里程约为350km，A与B车的平均速度之比为10∶7，A车的行驶时间比B车的少1h，那么两车的平均速度分别为多少？

查看解析收藏纠错

+选题
23. 小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：
项目
月功能费
基本话费
长途话费
短信费
金额/元
5

（1）该月小王手机话费共有多少元？

（2）扇形统计图中，表示短信费的扇形的圆心角为多少度？

（3）请将表格补充完整；

（4）请将条形统计图补充完整.

查看解析收藏纠错

+选题
24. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）
①画出△ABC关于x轴对称的△A₁B₁C₁ ，
②画出将△ABC绕原点O按逆时针旋转90°所得的△A₂B₂C₂ ，
③△A₁B₁C₁与△A₂B₂C₂成轴对称图形吗？若成轴对称图形，画出所有的对称轴；
④△A₁B₁C₁与△A₂B₂C₂成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标.

查看解析收藏纠错

+选题

25. 为缓解油价上涨给出租车待业带来的成本压力，某巿自2018年11月17日起，调整出租车运价，调整方案见下列表格及图像（其中a， b，c为常数）
行驶路程
收费标准
调价前
调价后
不超过3km的部分
起步价6元
起步价a 元
超过3km不超出6km的部分
每公里2.1元
每公里b元
超出6km的部分
每公里c元
设行驶路程xkm时，调价前的运价y₁（元），调价后的运价为y₂（元）如图，折线ABCD表示y₂与x之间的函数关系式，线段EF表示当0≤x≤3时，y₁与x的函数关系式，根据图表信息，完成下列各题：

（1）填空：a=，b=，c=.

（2）写出当x＞3时，y₁与x的关系，并在上图中画出该函数的图象.

（3）函数y₁与y₂的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由.

查看解析收藏纠错

+选题
26. 已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断
① OA＝OC ② AB＝CD ③ ∠BAD＝∠DCB ④ AD∥BC
请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：

（1）构造一个真命题，画图并给出证明；

（2）构造一个假命题，举反例加以说明.

查看解析收藏纠错

+选题

27. 已知二次函数的图象以A（－1，4）为顶点，且过点B（2，－5）

（1）求该函数的关系式；

（2）求该函数图象与坐标轴的交点坐标；

（3）将该函数图象向右平移，当图象经过原点时，A、B两点随图象移至A′、B′，求△O A′B′的面积.

查看解析收藏纠错

+选题
28. 如图1，一副直角三角板满足AB＝BC，AC＝DE，∠ABC＝∠DEF＝90°，∠EDF＝30°
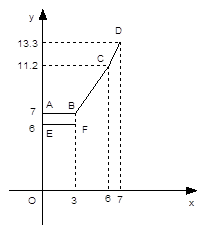
【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q

（1）【探究一】在旋转过程中，
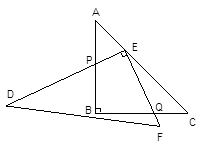
①如图2，当 $\text{[math]}$ 时，EP与EQ满足怎样的数量关系？并给出证明.
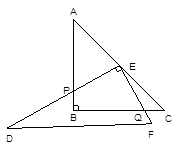
②如图3，当 $\text{[math]}$ 时E P与EQ满足怎样的数量关系？，并说明理由.
③根据你对（1）、（2）的探究结果，试写出当 $\text{[math]}$ 时，EP与EQ满足的数量关系式
为，其中 $\text{[math]}$ 的取值范围是(直接写出结论，不必证明)

（2）【探究二】若 $\text{[math]}$ 且AC＝30cm，连续PQ，设△EPQ的面积为S(cm²)，在旋转过程中：
①S是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.
②随着S取不同的值，对应△EPQ的个数有哪些变化？不出相应S值的取值范围.

查看解析收藏纠错

+选题

江苏省徐州巿2018年中考数学试卷

一、选择题

二、填空题

三、解答题

四、解答题

五、解答题

六、解答题

七、解答题

相关试卷收起∨

项目	月功能费	基本话费	长途话费	短信费
金额/元	5

行驶路程	收费标准
行驶路程	调价前	调价后
不超过3km的部分	起步价6元	起步价a 元
超过3km不超出6km的部分	每公里2.1元	每公里b元
超出6km的部分	每公里2.1元	每公里c元

江苏省徐州巿2018年中考数学试卷

一、选择题

二、填空题

三、解答题

四、解答题

五、解答题

六、解答题

七、解答题

相关试卷 收起∨

相关试卷收起∨