（人教版）2023-2024学年九年级上学期数学 23.1 图形的旋转期末复习(吉林地区专用)

1. 如图，在平面直角坐标系中，△ABC绕点C（0，1）旋转180°得到△A'B'C，已知点A的坐标为（2，-1）．则点A'的坐标是．（）

A . （- 2，1） B . （-2，3） C . （-2，-1） D . （-2，2）

查看解析收藏纠错

+选题
2. 如图，把△ABC绕C点顺时针旋转35°，得到△A'B'C，A'B'交AC于点D，若∠A'DC=90°，则∠A的度数（）

A . 35° B . 75° C . 55° D . 65°

查看解析收藏纠错

+选题
3. 如图，△ABC中，∠BAC=135°，把△ABC绕着点C顺时针旋转得到△DEC，若点D、A、B恰好在一条直线上，则下列结论错误的是（）

A . ED⊥BD B . △ABC≌△DEC C . $\text{[math]}$ D . BD＝CE+DE

查看解析收藏纠错

+选题
4. 如图所示的正六边形花环绕中必至少旋转 $\text{[math]}$ 度能与自身重合，则 $\text{[math]}$ 为（）

A . 30 B . 60 C . 120 D . 180

查看解析收藏纠错

+选题
5. 国旗上的五角星是旋转对称图形，它需要旋转（）后，才能与自身重合．

A . 36° B . 45° C . 60° D . 72°

查看解析收藏纠错

+选题
6. 如图，边长为1的正方形ABCD绕点A逆时针旋转45°后，得到正方形AB′C′D′，边B'C′与DC交于点O，则∠DOB'的度数为（　　）

A . 125° B . 130° C . 135° D . 140°

查看解析收藏纠错

+选题
7. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ ，点B的对应点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在△ABC中，∠ACB=90°，∠B=30°，AB=4，将△ABC绕点A顺时针旋转得到△AB'C'，当点C'落在边AB上时，线段CC'的长为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题

9. 如图，将△ABC绕点C逆时针旋转得到△A'B'C'，其中点A'与点A是对应点，点B'与点B是对应点，点B'落在边AC上，连结A'B．若∠ACB=45°，AC=2．BC=4，则∠A'B= °

查看解析收藏纠错

+选题
10. 如图，在等边△ABC中，点D是边AC上一点，将△BCD绕点B逆时针旋转60°得到△BAE，若BC=8，BD=6，则OAED的周长为

查看解析收藏纠错

+选题
11. 如图，该图形绕其中心旋转能与自身完全重合．则其旋转角最小为度．

查看解析收藏纠错

+选题
12. 如图所示的图形绕其中心至少旋转度就可以与原图形完全重合．

查看解析收藏纠错

+选题
13. 如图，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转角 $\text{[math]}$ ，得到 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

查看解析收藏纠错

+选题
14. 如图，E是正方形ABCD内一点，将△ABE绕点B顺时针旋转与△CBF重合，若BE= $\text{[math]}$ ，则EF=

查看解析收藏纠错

+选题

15. 如图，将矩形ABCD绕点A顺时针旋转得到矩形AB'C'D' ，点C的对应点C'恰好落在CB的延长线上，边AB与C'D'相交于点E．求证：BC=BC'．

查看解析收藏纠错

+选题
16. 如图，在△ABC中，AB=2，BC=3.6．∠B=60°，将△ABC绕点A按顺时针方向旋；转一定角度得到△ADK，当点B的对应点D恰好落在BC边上时，求CD的长．

查看解析收藏纠错

+选题
17. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为旋转中心，把 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
18. 如图，在Rt△ABC中，∠C=90°，∠BAC=30°，BC=2，以点B为旋转中心，把Rt△ABC逆时针旋转90°，得到△A'BC'，连接AA'，求AA'的长，

查看解析收藏纠错

+选题
19. 如图，在△ABD中，∠BAD=90°，将△ABD绕点A逆时针旋转后得到△ACE，C点落在BD边上，若∠E=17°，求∠BAC的度数．

查看解析收藏纠错

+选题
20. 如图，在Rt△ABC中，∠C= 90°，将△ABC绕着点B逆时针旋转得到△FBE，点C，A的对应点分别为E，F，点F落在BA上，连接AF．

（1）若∠BAC=40°，则∠AFE的度数为

（2）若AC=8，BC=6，求AF的长．

查看解析收藏纠错

+选题
21. 如图，在△ABC中，∠B=20°，∠ACB= =30°，AB=2 cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD的中点．

（1）指出旋转中心，并求出旋转的度数；

（2）求出∠BAE的度数和AE的长．

查看解析收藏纠错

+选题
22. 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转至 $\text{[math]}$ 处，使点B落在BC延长线上的D点处，求 $\text{[math]}$ 的度数．

查看解析收藏纠错

+选题
23. 如图，四边形 $\text{[math]}$ 是正方形，点 $\text{[math]}$ 为 $\text{[math]}$ 内一点，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的大小．

查看解析收藏纠错

+选题
24. 我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
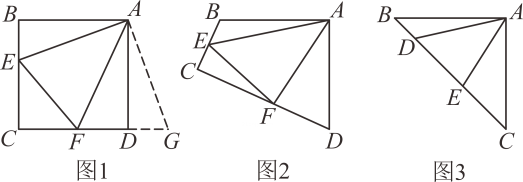
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上， $\text{[math]}$ ，连接EF ，则 $\text{[math]}$ ，试说明理由．

（1）思路梳理
$\text{[math]}$ ，
$\text{[math]}$ 把 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 至 $\text{[math]}$ ，可使AB与AD重合．
$\text{[math]}$ ，
$\text{[math]}$ ，点F、D、G共线．
根据，易证 $\text{[math]}$ ，得 $\text{[math]}$ ．

（2）类比引申
如图2，四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E、F分别在边BC、CD上， $\text{[math]}$ ，若 $\text{[math]}$ 、 $\text{[math]}$ 都不是直角，则当 $\text{[math]}$ 与 $\text{[math]}$ 满足等量关系时，仍有 $\text{[math]}$ ．

（3）联想拓展
如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D、E均在边BC上，且 $\text{[math]}$ ．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

查看解析收藏纠错

+选题

（人教版）2023-2024学年九年级上学期数学 23.1 图形的旋转期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

相关试卷收起∨

（人教版）2023-2024学年九年级上学期数学 23.1 图形的旋转 期末复习(吉林地区专用)

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

（人教版）2023-2024学年九年级上学期数学 23.1 图形的旋转期末复习(吉林地区专用)

相关试卷收起∨