山西省2023年中考数学试卷

1. 计算 $\text{[math]}$ 的结果为（）．

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 全民阅读有助于提升一个国家、一个民族的精神力量．图书馆是开展全民阅读的重要场所．以下是我省四个地市的图书馆标志，其文字上方的图案是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 山西是全国电力外送基地，2022年山西省全年外送电量达到1464亿千瓦时，同比增长 $\text{[math]}$ ．数据1464亿千瓦时用科学记数法表示为（）

A . $\text{[math]}$ 千瓦时 B . $\text{[math]}$ 千瓦时 C . $\text{[math]}$ 千瓦时 D . $\text{[math]}$ 千瓦时

查看解析收藏纠错

+选题
5. 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ 为对角线， $\text{[math]}$ 经过圆心 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 一种弹簧秤最大能称不超过 $\text{[math]}$ 的物体，不挂物体时弹簧的长为 $\text{[math]}$ ，每挂重 $\text{[math]}$ 物体，弹簧伸长 $\text{[math]}$ ．在弹性限度内，挂重后弹簧的长度 $\text{[math]}$ 与所挂物体的质量 $\text{[math]}$ 之间的函数关系式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心 $\text{[math]}$ 的光线相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为焦点．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 已知 $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，则a、b、c的关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 中国高铁的飞速发展，已成为中国现代化建设的重要标志．如图是高铁线路在转向处所设计的圆曲线（即圆弧），高铁列车在转弯时的曲线起点为 $\text{[math]}$ ，曲线终点为 $\text{[math]}$ ，过点 $\text{[math]}$ 的两条切线相交于点 $\text{[math]}$ ，列车在从 $\text{[math]}$ 到 $\text{[math]}$ 行驶的过程中转角 $\text{[math]}$ 为 $\text{[math]}$ ．若圆曲线的半径 $\text{[math]}$ ，则这段圆曲线 $\text{[math]}$ 的长为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 蜂巢结构精巧，其巢房横截面的形状均为正六边形．如图是部分巢房的横截面图，图中7个全等的正六边形不重叠且无缝隙，将其放在平面直角坐标系中，点 $\text{[math]}$ 均为正六边形的顶点．若点 $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 计算（ $\text{[math]}$ + $\text{[math]}$ ）（ $\text{[math]}$ ﹣ $\text{[math]}$ ）的结果为 .

查看解析收藏纠错

+选题
12. 如图是一组有规律的图案，它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，…依此规律，第n个图案中有个白色圆片（用含n的代数式表示）

查看解析收藏纠错

+选题
13. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ．以点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 的长为半径作弧交边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．分别以点 $\text{[math]}$ 为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交边 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
14. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》，它是儒家思想的核心著作，是中国传统文化的重要组成部分，若从这四部著作中随机抽取两本（先随机抽取一本，不放回，再随机抽取另一本），则抽取的两本恰好是《论语》和《大学》的概率是．

查看解析收藏纠错

+选题
15. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

查看解析收藏纠错

+选题

16.

（1）计算： $\text{[math]}$ ；

（2）计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
17. 解方程： $\text{[math]}$ ．

查看解析收藏纠错

+选题

18. 为增强学生的社会实践能力，促进学生全面发展，某校计划建立小记者站，有20名学生报名参加选拔．报名的学生需参加采访、写作、摄影三项测试，每项测试均由七位评委打分（满分100分），取平均分作为该项的测试成绩，再将采访、写作、摄影三项的测试成绩按 $\text{[math]}$ 的比例计算出每人的总评成绩．

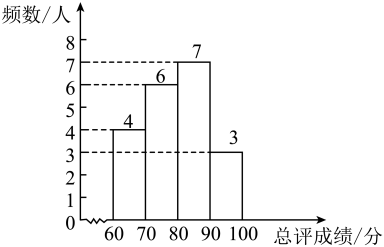
小悦、小涵的三项测试成绩和总评成绩如下表，这20名学生的总评成绩频数直方图（每组含最小值，不含最大值）如下图

选手	测试成绩/分			总评成绩/分
选手	采访	写作	摄影	总评成绩/分
小悦	83	72	80	78
小涵	86	84	▲	▲

（1）在摄影测试中，七位评委给小涵打出的分数如下：67，72，68，69，74，69，71．这组数据的中位数是分，众数是分，平均数是分；

（2）请你计算小涵的总评成绩；

（3）学校决定根据总评成绩择优选拔12名小记者．试分析小悦、小涵能否入选，并说明理由．

查看解析收藏纠错

+选题

19. 风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞．该大桥限重标志牌显示，载重后总质量超过30吨的车辆禁止通行．现有一辆自重8吨的卡车，要运输若干套某种设备，每套设备由1个A部件和3个B部件组成，这种设备必须成套运输．已知1个A部件和2个B部件的总质量为2.8吨，2个A部件和3个B部件的质量相等．

（1）求1个A部件和1个B部件的质量各是多少；

（2）卡车一次最多可运输多少套这种设备通过此大桥？

查看解析收藏纠错

+选题

20. 2023年3月，水利部印发《母亲河复苏行动河湖名单（2022－2025年）》，我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选．在推进实施母亲河复苏行动中，需要砌筑洛种驳岸（也叫护坡）．某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动，利用课余时间完成了实践调查，并形成了如下活动报告．请根据活动报告计算 $\text{[math]}$ 和 $\text{[math]}$ 的长度（结果精确到 $\text{[math]}$ ．参考数据： $\text{[math]}$ ， $\text{[math]}$ ）。

课题	母亲河驳岸的调研与计算
调查方式	资料查阅、水利部门走访、实地查看了解
	功能	驳岸是用来保护河岸，阻止河岸崩塌或冲刷的构筑物
	驳岸剖面图		相关数据及说明，图中，点A，B，C，D，E在同一竖直平面内， $\text{[math]}$ 与 $\text{[math]}$ 均与地面平行，岸墙 $\text{[math]}$ 于点A， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
	计算结果
交流展示

查看解析收藏纠错

+选题

21. 阅读与思考：下面是一位同学的数学学习笔记，请仔细阅读并完成相应任务．

瓦里尼翁平行四边形

我们知道，如图1，在四边形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 的中点，顺次连接 $\text{[math]}$ ，得到的四边形 $\text{[math]}$ 是平行四边形．

我查阅了许多资料，得知这个平行四边形 $\text{[math]}$ 被称为瓦里尼翁平行四边形．瓦里尼翁 $\text{[math]}$ 是法国数学家、力学家．瓦里尼翁平行四边形与原四边形关系密切．

①当原四边形的对角线满足一定关系时，瓦里尼翁平行四边形可能是菱形、矩形或正方形．

②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系．

③瓦里尼翁平行四边形的面积等于原四边形面积的一半．此结论可借助图1证明如下：

证明：如图2，连接 $\text{[math]}$ ，分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．

∵ $\text{[math]}$ 分别为 $\text{[math]}$ 的中点，∴ $\text{[math]}$ ．（依据1）

∴ $\text{[math]}$ ． ∵ $\text{[math]}$ ， ∴ $\text{[math]}$ ．

∵四边形 $\text{[math]}$ 是瓦里尼翁平行四边形，∴ $\text{[math]}$ ，即 $\text{[math]}$ ．

∵ $\text{[math]}$ ，即 $\text{[math]}$ ，

∴四边形 $\text{[math]}$ 是平行四边形．（依据2）∴ $\text{[math]}$ ．

∵ $\text{[math]}$ ， ∴ $\text{[math]}$ ．同理，…

任务：

（1）填空：材料中的依据1是指：．

依据2是指：．

（2）请用刻度尺、三角板等工具，画一个四边形 $\text{[math]}$ 及它的瓦里尼翁平行四边形 $\text{[math]}$ ，使得四边形 $\text{[math]}$ 为矩形；（要求同时画出四边形 $\text{[math]}$ 的对角线）

（3）在图1中，分别连接 $\text{[math]}$ 得到图3，请猜想瓦里尼翁平行四边形 $\text{[math]}$ 的周长与对角线 $\text{[math]}$ 长度的关系，并证明你的结论．

查看解析收藏纠错

+选题

22. 问题情境：“综合与实践”课上，老师提出如下问题：将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为 $\text{[math]}$ 和 $\text{[math]}$ ，其中 $\text{[math]}$ ．将 $\text{[math]}$ 和 $\text{[math]}$ 按图2所示方式摆放，其中点 $\text{[math]}$ 与点 $\text{[math]}$ 重合（标记为点 $\text{[math]}$ ）．当 $\text{[math]}$ 时，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．试判断四边形 $\text{[math]}$ 的形状，并说明理由．


（1）数学思考：谈你解答老师提出的问题；

（2）深入探究：老师将图2中的 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针方向旋转，使点 $\text{[math]}$ 落在 $\text{[math]}$ 内部，并让同学们提出新的问题．


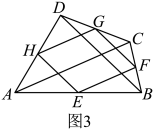
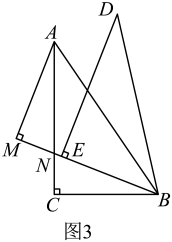
①“善思小组”提出问题：如图3，当 $\text{[math]}$ 时，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．试猜想线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并加以证明．请你解答此问题；



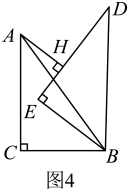
②“智慧小组”提出问题：如图4，当 $\text{[math]}$ 时，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．请你思考此问题，直接写出结果．



查看解析收藏纠错

+选题
23. 如图，二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴的正半轴交于点A，经过点A的直线与该函数图象交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点C．

（1）求直线 $\text{[math]}$ 的函数表达式及点C的坐标；

（2）点 $\text{[math]}$ 是第一象限内二次函数图象上的一个动点，过点 $\text{[math]}$ 作直线 $\text{[math]}$ 轴于点 $\text{[math]}$ ，与直线 $\text{[math]}$ 交于点D，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．
①当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；

②当点 $\text{[math]}$ 在直线 $\text{[math]}$ 上方时，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．设四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式，并求出S的最大值．

查看解析收藏纠错

+选题

山西省2023年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

山西省2023年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨