广东省深圳市罗湖区2022年九年级二模数学试题

修改时间：2024-07-13 浏览次数：148 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列几何体中，从正面看为三角形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 一个数的相反数-2，则这个数是（）

A . 2 B . $\text{[math]}$ 或-2 C . -2 D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 用不等式表示如图的解集，其中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 冬季来临，某同学对甲、乙、丙、丁四个菜市场第四季度的白菜价格进行调查．四个菜市第四个季度白菜的平均值均为2.50元，方差分别为S_甲²＝18.3，S_乙²＝17.4，S_丙²＝20.1，S_丁²＝12.5．第四季度白菜价格最稳定的菜市场是（）.

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
5. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 在Rt△ABC中，∠C＝90°，如果AB＝2，BC＝1，那么sinB的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在长为32米、宽为20米的矩形地面上修筑同样宽的道路（图中阴影部分），余下部分种植草坪，要使小路的面积为100平方米，设道路的宽 $\text{[math]}$ 米，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 下列命题是真命题的是（）

A . 平行四边形的对角互补 B . 对角线相等的四边形是矩形 C . 相似三角形的面积比等于对应高的比 D . 位似三角形是相似三角形

查看解析收藏纠错

+选题
9. 如图，AB是圆O的直径，C，D是AB上的两点，连接AC，BD相交于点E，若∠BEC＝56°，那么∠DOC的度数为（）

A . 28° B . 56° C . 64° D . 68°

查看解析收藏纠错

+选题
10. 如图，正方形ABCD的边长为4，点E在边CD上，且CE=1，连结AE，点F在边AD上，连结BF，把 $\text{[math]}$ 沿BF翻折，点A恰好落在AE上的点G处，下列结论：①AE=BF；②AD=3DF；③ $\text{[math]}$ ；④GE=0.2，其中正确的是（）

A . ①②③④ B . ①③④ C . ①②③ D . ①③

查看解析收藏纠错

+选题

二、填空题

11. 分解因式： $\text{[math]}$

查看解析收藏纠错

+选题
12. 在一个不透明纸箱中放有除了数字不同外，其它完全相同的2张卡片，分别标有数字1、2，从中任意摸出一张，放回搅匀后再任意摸出一张，两次摸出的数字之积为偶数的概率为．

查看解析收藏纠错

+选题
13. 如图，在 $\text{[math]}$ 中，分别以A、B为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧交于P、Q两点，直线PQ交BC于点D，连接AD；再分别以A、C为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧交于M，N两点，直线MN交BC于点E，连接AE．若 $\text{[math]}$ 的周长为17，则BD的长为．

查看解析收藏纠错

+选题
14. 如图， $\text{[math]}$ 、 $\text{[math]}$ 是函数 $\text{[math]}$ 上两点， $\text{[math]}$ 为一动点，作 $\text{[math]}$ 轴， $\text{[math]}$ 轴，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 如图， $\text{[math]}$ 中，以点O为圆心， $\text{[math]}$ 为半径作 $\text{[math]}$ ，边 $\text{[math]}$ 与 $\text{[math]}$ 相切于点A，把 $\text{[math]}$ 绕点A逆时针旋转得到 $\text{[math]}$ ，点O的对应点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 上，则 $\text{[math]}$ 的值是．

查看解析收藏纠错

+选题

三、解答题

16. 解方程， $\text{[math]}$ .

查看解析收藏纠错

+选题
17. 某校760名学生参加植树活动，要求每人植树的范围是2≤x≤5棵，活动结束后随机抽查了若名学生每人的植树量，并分为四种类型，A：2棵；B：3棵；C：4棵；D：5棵，将各类的人数绘制成扇形统计图（如图2）和条形统计图（如图1）．回答下列问题：

（1）补全条形统计图；

（2）被调查学生每人植树量的众数、中位数分别是多少？

（3）估计该校全体学生在这次植树活动中共植树多少棵？

查看解析收藏纠错

+选题
18. 在坐标系中作出函数y＝x＋2的图象，根据图象回答下列问题：

（1）方程x＋2＝0的解是；

（2）不等式x＋2＞1的解；

（3）若﹣2≤y≤2，则x的取值范围是．

查看解析收藏纠错

+选题
19. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， E是BC的中点，以AC为直径的 $\text{[math]}$ 与AB边交于点D，连接DE．

（1）求证：DE是 $\text{[math]}$ 的切线；

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 直径的长．

查看解析收藏纠错

+选题
20. 69中学计划购买A、B两种学习用品奖励学生，已知购买一个A比购买一个B多用20元，若用400元购买A的数量是用160元购买B数量的一半，

（1）求A、B两种学习用品每件多少钱？

（2）经商谈，商店给该校购买一个A奖品赠送一个B奖品的优惠，如果该校需要B奖品的个数是A奖品个数的2倍还多8个，且该学校购买A、B两种奖品的总费用不超过670元，那么该校最多可购买多少个A奖品？

查看解析收藏纠错

+选题
21. 如图

（1）【探索发现】
如图①，是一张直角三角形纸片，∠B=90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其符合题意性，并得出：矩形的最大面积与原三角形面积的比值为．

（2）【拓展应用】
如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为．（用含a，h的代数式表示）

（3）【灵活应用】
如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．

（4）【实际应用】
如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC= $\text{[math]}$ ，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．

查看解析收藏纠错

+选题
22. 九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践——应用——探究的过程

（1）实践：他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量，测得隧道的路面宽为10米，隧道顶部最高处距地面6.25米，并画出了隧道截面图，建立了如图1所示的直角坐标系，请你求出抛物线的解析式

（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖起方向上的高度差至少为0.5米，为了确保安全，问该隧道能否让最宽3米，最高3.5米的两辆车居中并列行驶（不考虑两车之间的空隙）？

（3）探究：该课题学习小组为进一步探究抛物线的有关知识，他们借助上述抛物线模型，提出了以下两个问题，请予解答：
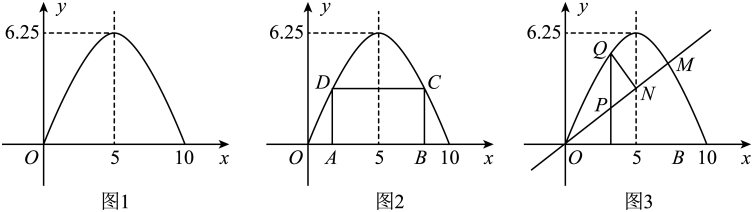
①如图2，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上，顶点A、B落在x轴上，设矩形ABCD的周长为为l，求l的最大值
②如图3，过原点作一条直线y=x，交抛物线于M，交抛物线的对称轴于N，P为直线OM上一动点，过点P作x轴的垂线交抛物线于点Q，问在直线OM上是否存在点P，使以点P、N、Q为顶点的三角形为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由

查看解析收藏纠错

+选题

广东省深圳市罗湖区2022年九年级二模数学试题

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨