湘教版初中数学九年级上学期期末复习专题16 总体平均数与方差的估计

1. 某班在体育活动中，测试了十位学生的“一分钟跳绳”成绩，得到十个各不相同的数据.在统计时，出现了一处错误：将最高成绩写得更高了，则计算结果不受影响的是（）

A . 平均数 B . 中位数 C . 方差 D . 众数

查看解析收藏纠错

+选题
2. 计划从甲、乙、丙、丁四人中选出一人参加射击比赛，经过三轮的初赛，他们的平均成绩都是9环，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，从成绩稳定上看，你认为谁会去最合适（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
3. 下列说法正确的是（）

A . 了解市民知晓“礼让行人”交通新规的情况，适合全面调查 B . 一组数据5，5，3，4，1的中位数是3 C . 甲、乙两人9次跳高成绩的方差分别为 $\text{[math]}$ _甲² $\text{[math]}$ ， $\text{[math]}$ _乙² $\text{[math]}$ ，说明乙的成绩比甲稳定 D . “经过有交通信号灯的路口，遇到红灯”是随机事件

查看解析收藏纠错

+选题
4. 今年是三年禁毒“大扫除”攻坚克难之年.为了让学生认识毒品的危害，某校举办了禁毒知识比赛，小红所在班级学生的平均成绩是80分，小星所在班级学生的平均成绩是85分，在不知道小红和小星成绩的情况下，下列说法比较合理的是（）

A . 小红的分数比小星的分数低 B . 小红的分数比小星的分数高 C . 小红的分数与小星的分数相同 D . 小红的分数可能比小星的分数高

查看解析收藏纠错

+选题
5. 某校评选先进班集体，从“学习”、“卫生”“纪律”、“活动参与j”四个方面综合考核打分，各项满分均为100，所占比例如下表：

项目

学习

卫生

纪律

活动参与

所占比例

40%

25%

25%

10%

某班这四项得分依次为85，90，80，75，则该班四项综合得分为（）

A . 84 B . 83.5 C . 83 D . 82.5

查看解析收藏纠错

+选题

6. 甲、乙、丙、丁四名射击运动员进行奥运选拔赛，每人10次射击成绩的平均数（单位：环）及方差 $\text{[math]}$ （单位：环）如下表所示：

	甲	乙	丙	丁
$\text{[math]}$	9	8	9	9
$\text{[math]}$	1.6	0.8	3	0.8

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题

7. 某同学连续7天测得体温（单位： $\text{[math]}$ ）分别是：36.5、36.3、36.7、36.5、36.7、37.1、37.1，关于这一组数据，下列说法正确的是（）

A . 众数是36.3 B . 中位数是36.6 C . 方差是0.08 D . 方差是0.09

查看解析收藏纠错

+选题
8. 一组数据8，7，8，6，4，9的中位数和平均数分别是（）

A . 7和8 B . 7.5和7 C . 7和7 D . 7和7.5

查看解析收藏纠错

+选题

9. 某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛，在选拔比赛中，每人射击10次，他们10次成绩的平均数及方差如下表所示：

	甲	乙	丙	丁
平均数/环	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
方差/环 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

请你根据表中数据选一人参加比赛，最合适的人选是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题

10. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都约为8.8环，方差分别为S $\text{[math]}$ = 0.63环² ， S $\text{[math]}$ = 0.51环² ， S $\text{[math]}$ = 0.48环² ， S $\text{[math]}$ = 0.42环² ，则四人中成绩最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题

11. 一组数据0，1，3，2，4的平均数是，这组数据的方差是.

查看解析收藏纠错

+选题
12. 已知一组数据1，a，3，6，7，它的平均数是5，这组数据的方差是.

查看解析收藏纠错

+选题

13. 某校欲招聘一名数学教师，学校对甲乙丙三位候选人进行三项能力测试，各项成绩满分均为100分，根据结果择优录用，三位候选人测试成绩如表：

测试项目	成绩
测试项目	甲	乙	丙
教学能力	77	73	73
科研能力	70	71	65
组织能力	64	72	84

根据实际需要学校将三项能力测试得分按6：2：2的比例确定每人的成绩，将被录用的是

查看解析收藏纠错

+选题

14. 某广告公司决定招聘广告策划人员一名，应聘者小李笔试、面试、创意三项素质测试的成绩分别是90分、80分和85分，若将这三项成绩分别按 $\text{[math]}$ 的比例计算，则小李的最后得分是分.

查看解析收藏纠错

+选题
15. “绿水青山就是金山银山”为了响应党中央对环境保护的号召，某校要从报名的甲、乙、丙三人中选取一人去参加南宁市举办的环保演讲比赛经过两轮初赛后，甲、乙、丙三人的平均成绩都是89，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .你认为参加决赛比较合适.

查看解析收藏纠错

+选题
16. 甲、乙两名同学进行跳高测试，每人跳10次，他们的平均成绩都是1.55米，方差分别是 $\text{[math]}$ =1.2， $\text{[math]}$ =5，则在本次测试中同学的成绩更稳定(填“甲”或“乙”)

查看解析收藏纠错

+选题

17. 为庆祝中国共产党建党100周年，某校举行了“红色华诞，党旗飘扬”党史知识竞赛.为了解竞赛成绩，抽样调查了七，八年级部分学生的分数，过程如下：

（ 1 ）收集数据从该校七.八年级学生中各随机抽取20名学生的分数，其中八年级的分数如下：

81 83 84 85 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

（ 2 ）整理、描述数据按如下分段整理描述样本数据：

分数 $\text{[math]}$

人数

年级

$\text{[math]}$

七年级

4

6

2

8

八年级

3

$\text{[math]}$

4

7

（ 3 ）分析数据两组样本数据的平均数、中位数、众数、方差如下表所示：

年级	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$\text{[math]}$	$\text{[math]}$	33.2

根据以上提供的信息，解答下列问题：

①填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

②样本数据中，七年级甲同学和八年级乙同学的分数都为90分，同学的分数在本年级抽取的分数中从高到低排序更靠前（填“甲”或“乙”）：

③从样本数据分析来看，分数较整齐的是年级（填“七”或“八”）；

④如果七年级共有400人参赛，则该年级约有人的分数不低于95分.

查看解析收藏纠错

+选题

18. 某校为了解八年级学生参加社会实践活动情况，随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：

（Ⅰ）本次接受随机抽样调查的学生人数为 ▲ ，图①中的m的值为 ▲ ；

（Ⅱ）求本次抽样调查获取的样本数据的众数、中位数和平均数；

（Ⅲ）若该校八年级学生有240人，估计参加社会实践活动时间大于7天的学生人数．

查看解析收藏纠错

+选题
19. 某学校为了了解本校1200名学生的课外阅读的情况，现从各年级随机抽取了部分学生，对他们一周的课外阅读时间进行了调整，井绘制出如下的统计图①和图②，根据相关信息，解答下列问题：

（1）本次接受随机抽样调查的学生人数为，图①中 $\text{[math]}$ 的值为；

（2）求本次调查获取的样本数据的众数、中位数和平均数；

（3）根据样本数据，估计该校一周的课外阅读时间大于 $\text{[math]}$ 的学生人数．

查看解析收藏纠错

+选题

20. 我校在七、八年级举行了“新冠疫情防控”知识竞赛，从七、八年级各随机抽取了10名学生进行比赛（百分制）．测试成绩整理、描述和分析如下：（成绩得分用x表示，共分成四组：A． $\text{[math]}$ B． $\text{[math]}$ C． $\text{[math]}$ D． $\text{[math]}$ ）

七年级10名学生的成绩：96，86，96，86，99，96，90，100，89，82．

八年级10名学生的成绩在C组中的数据是：94，90，92．下表为七、八年级抽取的学生竞赛成绩统计表

年级	平均数	中位数	众数	方差
七年级	92	b	c	d
八年级	92	93	100	50.4

根据以上信息，解答下列问题：

（1） $\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$

（2）这次比赛中那个年级成绩更稳定？说明理由：

（3）我校八年级共1200人参加了此次调查活动，估计参加此次调查活动成绩优秀（ $\text{[math]}$ ）的八年级学生人数是多少？

查看解析收藏纠错

+选题

21. 某校260名学生参加植树活动要求每人植4~7棵活动结束后随机抽查了20名学生每人的植树量，并分成四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形统计图（如图1所示）和条形统计图（如图2所示），经确认扇形统计图是正确的，而条形统计图尚有一处不符合题意．

回答下列问题：

（1）写出条形统计图中存在的错误，并说明理由；

（2）直接写出这20名同学每人植树量的中位数；

（3）在求这20名同学每人植树量的平均数时，小宇是这样分析的：

第一步：求平均数的公式是 $\text{[math]}$ ；

第二步：在该问题中， $\text{[math]}$ ；

第三步： $\text{[math]}$ （棵）．

小宇的分析存在错误，请帮助他求出正确的平均数，并估计这260名学生共植树多少棵？

查看解析收藏纠错

+选题
22. 重庆一中的食堂素有“中学食堂排行榜第一名”的美称，一食堂的烧菜、二食堂的串串、三食堂的夜宵，让无数一中学子毕业后魂牵梦绕.每一道食物的烹饪离不开勤劳的厨师们，也离不开食堂采购人员精心的挑选.现有甲、乙两家肉禽类公司到我校推销鸡腿，两家鸡腿价格相同，品质相似.学校决定通过评估质量来确定选择哪家鸡腿，检查人员从两家分别抽取了100个鸡腿，然后再从中随机各抽取20个，这些鸡腿的质量记为x（单位：克），将所得的数据分为5组（A组： $\text{[math]}$ ；B组： $\text{[math]}$ C组： $\text{[math]}$ ；D组： $\text{[math]}$ ；E组： $\text{[math]}$ ）.学校对数据进行分析后，得到如下部分信息：
a.甲公司被抽取的20个鸡腿质量频数分布直方图

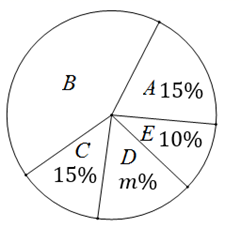
b.乙公司被抽取的20个鸡腿质量扇形统计图

c.甲公司被抽取的鸡腿质量在 $\text{[math]}$ 这一组的数据是：75 76 78 76 77 78 79

d.乙公司被抽取的鸡腿质量在 $\text{[math]}$ 这一组的数据是：75 78 75 75 75 77 76 75

e.甲、乙公司被抽取的鸡腿质量的平均数、中位数、众数如下：

公司

甲公司

乙公司

平均数

73

73

中位数

n

75

众数

74

$\text{[math]}$

根据以上信息，解答下列问题：

（1）直接写出上述表中m，n，k的值；

（2）根据以上数据，请估算乙公司这100个鸡腿中质量不低于75克的数量；

（3）根据以上数据分析，如果你是食堂采购人员，你会选择采购哪个公司的鸡腿，请说明理由（写出一条理由即可）.

查看解析收藏纠错

+选题

湘教版初中数学九年级上学期期末复习专题16 总体平均数与方差的估计

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

项目	学习	卫生	纪律	活动参与
所占比例	40%	25%	25%	10%

公司	甲公司	乙公司
平均数	73	73
中位数	n	75
众数	74	$\text{[math]}$

湘教版初中数学九年级上学期期末复习专题16 总体平均数与方差的估计

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨