2022年苏科版初中数学《中考一轮复习》专题三函数 3.5 一次函数的应用

1. 暑假期间，小宇和小华相约到奥林匹克森林公园参加健步走活动，小华在小宇前方1800米处，二人同时出发，沿相同方向步行．走了40分钟时，小华先到达终点等候小宇，10分钟后，小宇也到达终点．在整个行走过程中，小宇和小华均保持各自的速度匀速行走，二人相距的路程 $\text{[math]}$ （米）与小宇出发的时间 $\text{[math]}$ （分钟）之间的关系如图所示，下列说法中，错误的是（）

A . 小宇的速度是100米/分 B . 出发时，小宇距离终点5000米 C . 当小宇走了25分钟时，两人的距离为1200米 D . 当小宇走了3000米时，小华恰好离终点800米

查看解析收藏纠错

+选题
2. 为了解脱贫攻坚成果，宣传乡村振兴发展之路，某电视台记者乘汽车赴360km外的新农村进行采访，路程的前一部分为高速公路，后一部分为省道．若汽车在高速公路和省道上分别以某一速度匀速行驶，汽车行驶的路程y（单位：km）与时间x（单位：h）之间的关系如图所示，则下列结论正确的是（）

A . 汽车在高速公路上的行驶速度为180km/h B . 省道总长为90km C . 汽车在省道上的行驶速度为60km/h D . 该记者在出发3.5h后到达采访地

查看解析收藏纠错

+选题
3. 如图是甲、乙两车在某时段速度随时间变化的图象，下列结论正确的是（）

A . 乙前3秒行驶的路程为15米 B . 在0到6秒内甲的速度每秒增加6米/秒 C . 两车到第2.5秒时行驶的路程相等 D . 在0至6秒内甲的速度都大于乙的速度

查看解析收藏纠错

+选题
4. 已知A，B两地相距60km，甲、乙两人沿同一条公路从A地出发到B地，甲骑自行车匀速行驶3h到达，乙骑摩托车.比甲迟1h出发，行至30km处追上甲，停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地（）

A . 15km B . 16km C . 44km D . 45km

查看解析收藏纠错

+选题
5. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步，先到终点的人原地休息．已知甲先出发3秒，在跑步过程中甲、乙两人之间的距离 $\text{[math]}$ (米)与乙出发的时间x(秒)之间的函数关系如图所示，正确的个数为（）
①乙的速度为5米/秒；②离开起点后，甲、乙两人第一次相遇时，距离起点12米；③甲、乙两人之间的距离超过32米的时间范围是 $\text{[math]}$ ；④乙到达终点时，甲距离终点还有68米．

A . 4 B . 3 C . 2 D . 1

查看解析收藏纠错

+选题
6. 甲、乙两地之间是一条直路，在全民健身活动中，小明跑步从甲地前往乙地，一段时间后，小亮骑自行车从乙地前往甲地，两人都保持匀速.小亮先到达目的地，两人之间的距离y（km）与小明运动的时间t（h）的函数关系大致如图所示，则下列说法不正确的是（）

A . 小明比小亮先出发36分钟 B . 小明的速度为10km/h C . 小亮的速度为20km/h D . 小亮出发1h后与小明相遇

查看解析收藏纠错

+选题
7. 在我国川西高原某山脉间有一河流，当河流中的水位上升到一定高度时因河堤承压有溃堤的危险．于是水利工程师在此河段的某处河堤上修了一个排水的预警水库联通另一支流．当河流的水位超过警戒位时就有河水流入预警的水库中，当水库有一定量的积水后，就会自动打开水库的排水系统流入另一支流．当河流的水位低于警戒位时水库的排水系统的排水速度则变慢．假设预警水库的积水时间为 $\text{[math]}$ 分钟，水库中积水量为 $\text{[math]}$ 吨，图中的折线表示某天 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系，下列说法中：
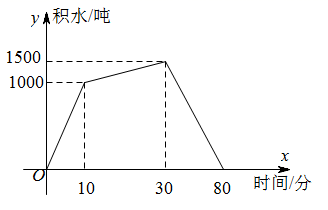
①这天预警水库排水时间持续了80分钟；②河流的水位超过警戒位时预警水库的排水速度比进水速度少25吨/分；③预警水库最高积水量为1500吨；④河流的水位低于警戒位时预警水库的排水速度为30吨/分．其中正确的信息判断是（）

A . ①④ B . ①③ C . ②③ D . ②④

查看解析收藏纠错

+选题
8. 从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进，已知小明骑车上坡的速度比在平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km.设小明出发xh后，到达离甲地ykm的地方，图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h②小明途中休息了0.1h；③小明从甲地去乙地来回过程中，两次经过距离甲地5.5km的地方的时间间隔为0.15h则以上说法中正确的个数为（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
9.
甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：

①a=40，m=1；
②乙的速度是80km/h；
③甲比乙迟 $\text{[math]}$ h到达B地；
④乙车行驶 $\text{[math]}$ 小时或 $\text{[math]}$ 小时，两车恰好相距50km．

正确的个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
10. 如图，在梯形ABCD中，AB=BC=10cm，CD=6cm，∠C=∠D-90°，动点P、Q同时以每秒1cm的速度从点B出发，点P沿BA、AD、DC运动，点Q沿BC、CD运动，P点与Q点相遇时停止，设P、Q同时从点B出发x秒时，P、Q经过的路径与线段PQ围成的图形的面积为y（cm²），则y与x之间的函微关系的大致图象为（）

A . B . C . D .

查看解析收藏纠错

+选题

11. 如图，一辆汽车和一辆摩托车分别从A ， B两地去同一城市C ，它们离A地的路程随时间变化的图象如图所示，则两车相遇时距离C地还有千米．

查看解析收藏纠错

+选题
12. 甲、乙两人分别从A、B两地出发，相向而行．图中的 $\text{[math]}$ ， $\text{[math]}$ 分别表示甲、乙离B地的距离 $\text{[math]}$ 与甲出发后所用时间 $\text{[math]}$ 的函数关系图象，则甲出发小时与乙相遇．

查看解析收藏纠错

+选题
13. 小张、小王两个人从甲地出发，去8千米外的乙地，图中线段OA、PB分别反映了小张、小王步行所走的路程S（千米）与时间t（分钟）的函数关系，根据图象提供的信息，小王比小张早到乙地的时间是分钟．

查看解析收藏纠错

+选题
14. 甲、乙两车分别从 $\text{[math]}$ 地、 $\text{[math]}$ 地同时向 $\text{[math]}$ 地匀速行驶 $\text{[math]}$ 在 $\text{[math]}$ 两地之间）.甲追上乙之后，乙立即以原来速度的2倍向 $\text{[math]}$ 地继续行驶，且此刻速度大于甲的速度，到达 $\text{[math]}$ 地后立即以提高后的速度返回 $\text{[math]}$ 地，甲车到达 $\text{[math]}$ 地后立即以原来速度返回 $\text{[math]}$ 地，两车距 $\text{[math]}$ 地的距离之和 $\text{[math]}$ （千米）与甲车行驶的时间 $\text{[math]}$ 小时）之间的部分函数关系如图所示，那么甲、乙两车第二次相遇时甲行驶的时间是小时.

查看解析收藏纠错

+选题
15. 甲、乙两车从A地出发，匀速驶向B地，甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶.乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇.在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示.给出下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.5.其中说法正确的有.（把你认为正确结论的序号都填上）

查看解析收藏纠错

+选题
16. 已知 $\text{[math]}$ 、 $\text{[math]}$ 两地相距200千米，货车甲从 $\text{[math]}$ 地出发将一批物资运往 $\text{[math]}$ 地，行驶一段路程后出现故障，即刻停车与 $\text{[math]}$ 地联系. $\text{[math]}$ 地收到消息后立即派货车乙从 $\text{[math]}$ 地出发去接运甲车上的物资，货车乙遇到货车甲后，用了30分钟将物资从货车甲搬运到货车乙上，随后以原速开往 $\text{[math]}$ 地，货车甲以原速的 $\text{[math]}$ 返回 $\text{[math]}$ 地.两辆货车之间的路程 $\text{[math]}$ 与货车甲出发的时间 $\text{[math]}$ 的函数关系如图所示（通话等其他时间忽略不计）.若点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是.

查看解析收藏纠错

+选题
17. 为了做到合理用药，使药物在人体内发挥疗效作用，该药物的血药浓度应介于最低有效浓度与最低中毒浓度之间．某成人患者在单次口服1单位某药后，体内血药浓度及相关信息如图：

根据图中提供的信息，下列关于成人患者使用该药物的说法中：

①首次服用该药物1单位约10分钟后，药物发挥疗效作用；

②每间隔4小时服用该药物1单位，可以使药物持续发挥治疗作用；

③每次服用该药物1单位，两次服药间隔小于2.5小时，不会发生药物中毒．

所有正确的说法是．

查看解析收藏纠错

+选题
18. 小刚从家出发匀速步行去学校上学.几分钟后发现忘带数学作业，于是掉头原速返回并立即打电话给爸爸，挂断电话后爸爸立即匀速跑步去追小刚，同时小刚以原速的两倍匀速跑步回家，爸爸追上小刚后以原速的 $\text{[math]}$ 倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校，并在从家出发后23分钟到校（小刚被爸爸追上时交流时间忽略不计）.两人之间相距的路程y（米）与小刚从家出发到学校的步行时间x（分钟）之间的函数关系如图所示，则小刚家到学校的路程为米.

查看解析收藏纠错

+选题

19.
某市规定了每月用水18立方米以内（含18立方米）和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x（立方米）的函数，其图象如图所示.

（1）若某月用水量为18立方米，则应交水费多少元？

（2）求当x>18时，y关于x的函数表达式.若小敏家某月交水费81元，则这个月用水量为多少立方米？

查看解析收藏纠错

+选题
20. 为发展旅游经济，我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人，非节假日打a折售票，节假日按团队人数分段定价售票，即m人以下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人部分的游客打b折售票.设某旅游团人数为x人，非节假日购票款为y₁（元），节假日购票款为y₂（元）.y₁与y₂之间的函数图象如图所示.

（1）观察图象可知：a＝；b＝；m＝；

（2）求出y₁ ， y₂与x之间的函数关系式.

查看解析收藏纠错

+选题
21. 已知A、B两地相距 $\text{[math]}$ ，一辆货车从A地前往B地，途中因装载货物停留一段时间．一辆轿车沿同一条公路从B地前往A地，到达A地后（在A地停留时间不计）立即原路原速返回．如图是两车距B地的距离 $\text{[math]}$ 与货车行驶时间 $\text{[math]}$ 之间的函数图象，结合图象回答下列问题：

（1）图中m的值是；轿车的速度是 $\text{[math]}$ ；

（2）求货车从A地前往B地的过程中，货车距B地的距离 $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数关系式；

（3）直接写出轿车从B地到A地行驶过程中，轿车出发多长时间与货车相距 $\text{[math]}$ ？

查看解析收藏纠错

+选题
22.
在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y₁、y₂（km），y₁、y₂与x的函数关系如图所示．
（1）填空：A、C两港口间的距离为多少km，a 等于多少；
（2）求图中点P的坐标，并解释该点坐标所表示的实际意义；
（3）若两船的距离不超过10km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．

查看解析收藏纠错

+选题
23.
甲、乙两车分别从A、B两地同时出发相向而行，并以各自的速度匀速行驶，甲车与乙车相遇后休息半小时，再按原速度继续前进到达B地；乙车从B地直接到达A地；两车到达各自目的地后即停止．如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
（1）甲车的速度，m等于多少；
（2）请分别写出两车在相遇前到B地的距离y（千米）与甲车出发时间x（小时）的函数关系式；
（3）当乙车行驶多少时间时，甲乙两车的距离是280千米．

查看解析收藏纠错

+选题
24.
清明小长假期间，小明和小亮相约从学校出发，去距学校6千米的三国古城遗址公园游玩，小明步行但小亮骑自行车，在去公园的全过程中，骑自行车的小亮同学比步行的小明同学少用40分钟，已知骑自行车的速度是步行速度的3倍．
（1）求小明同学每分钟走多少千米？
（2）右图是两同学前往公园时的路程y（千米）与时间x（分钟）的函数图象．
完成下列填空：
①表示小亮同学的函数图象什么线段；
②已知A点坐标（30，0），则B点的坐标为多少．

查看解析收藏纠错

+选题
25.
从甲地到乙地，先是一段上坡路，然后是一段平路，小明骑车从甲地出发，到达乙地后休息一段时间，然后原路返回甲地．假设小明骑车在上坡、平路、下坡时分别保持匀速前进，已知小明骑车上坡的速度比平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km，设小明出发xh后，到达离乙地ykm的地方，图中的折线ABCDEF表示y与x之间的函数关系．
（1）小明骑车在平路上的速度为多少km/h，他在乙地休息了多少小时．
（2）分别求线段AB、EF所对应的函数关系式．
（3）从甲地到乙地经过丙地，如果小明两次经过丙地的时间间隔为0.85h，求丙地与甲地之间的路程．

查看解析收藏纠错

+选题
26.
甲、乙两车分别从A，B两地同时出发相向而行．并以各自的速度匀速行驶，甲车途经C地时休息一小时，然后按原速度继续前进到达B地；乙车从B地直接到达A地，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
（1）直接写出a，m，n的值；
（2）求出甲车与B地的距离y（千米）与甲车出发时间x（小时）的函数关系式（写出自变量x的取值范围）；
（3）当两车相距120千米时，乙车行驶了多长时间？

查看解析收藏纠错

+选题
27. 疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $\text{[math]}$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $\text{[math]}$ （万人）与各自接种时间 $\text{[math]}$ （天）之间的关系如图所示．

（1）直接写出乙地每天接种的人数及 $\text{[math]}$ 的值；

（2）当甲地接种速度放缓后，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式，并写出自变量 $\text{[math]}$ 的取值范围；

（3）当乙地完成接种任务时，求甲地未接种疫苗的人数．

查看解析收藏纠错

+选题
28.
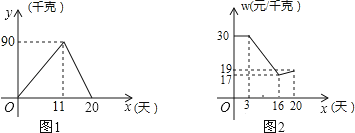
小明家今年种植的草莓喜获丰收，采摘上市20天全部销售完，爸爸让他对今年的销售情况进行跟踪记录，小明利用所学的数学知识将记录情况绘成图象（所得图象均为线段），日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，草莓的价格w（单位：元/千克）与上市时间x（单位：天）的函数关系如图2所示．
（1）观察图象，直接写出当0≤x≤11时，日销售量y与上市时间x之间的函数解析式为；当11≤x≤20时，日销售量y与上市时间x之间的函数解析式为．
（2）试求出第11天的销售金额；
（3）若上市第15天时，爸爸把当天能销售的草莓批发给了邻居马叔叔，批发价为每千克15元，马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完，他在销售的过程中，草莓总质量损耗了2%．那么，马叔叔支付完来回车费20元后，当天能赚到多少元？

查看解析收藏纠错

+选题

2022年苏科版初中数学《中考一轮复习》专题三函数 3.5 一次函数的应用

一、单选题

二、填空题

三、解答题

相关试卷收起∨

2022年苏科版初中数学《中考一轮复习》专题三 函数 3.5 一次函数的应用

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

2022年苏科版初中数学《中考一轮复习》专题三函数 3.5 一次函数的应用

相关试卷收起∨