修改时间:2021-11-16 浏览次数:100 类型:复习试卷
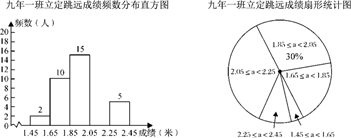
选课情况进行统计后,制成了两幅不完整的统计图 (如图).

4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“兵”字面朝上频数 | 14 | 38 | 47 | 52 | 66 | 78 | 88 | |
相应频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.56 | 0.55 |
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“兵”字面朝上频数 | 14 | | 38 | 47 | 52 | 66 | 78 | 88 |
相应频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | | 0.56 | 0.55 |
画出“兵”字面朝上的频率分布折线图;

某种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 12 | 24 | 12 |
试题篮