初中数学暑假作业（人教版：八年级升九年级）：05第二十章数据的分析复习题

修改时间：2021-07-07 浏览次数：106 类型：复习试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 我市某一周每天的最高气温统计如下（单位：℃）：27，28，29，28，29，30，29，这一组数据的众数与中位数分别是（）

A . 28，28 B . 28，29 C . 29，28 D . 29，29

查看解析收藏纠错

+选题
2. 某篮球队5名场上队员的身高(单位：cm)分别是183、187、190、200、195，现用-名身高为210cm的队员换下场上身高为195cm的队员，与换人前相比，场上队员身高的（）

A . 平均数变大，方差变小 B . 平均数变小，方差变大 C . 平均数变大，方差变大 D . 平均数变小，方差变小

查看解析收藏纠错

+选题
3. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为 $\text{[math]}$ =0.56， $\text{[math]}$ =0.60， $\text{[math]}$ =0.50， $\text{[math]}$ =0.44，则成绩最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
4. 已知一组数据：2，5， $\text{[math]}$ ，7，9的平均数是6，则这组数据的众数是（）.

A . 9 B . 7 C . 5 D . 2

查看解析收藏纠错

+选题
5. 在一次“爱心捐助”捐款活动中，某班第一小组8名同学捐款的金额(单位：元）如表所示，则这 $\text{[math]}$ 名同学捐款的平均金额为（）

金额/元

5

6

7

10

人数

2

3

2

1

A . 6.5元 B . 6元 C . 3.5元 D . 7元

查看解析收藏纠错

+选题
6. 小明已求出了五个数据：6，4，3，4，□的平均数，在计算它们的方差时，出现了这一步：(3-5)²+(4-5)²+(4-5)²+(6-5)²+（□- 5)*=16(□是后来被遮挡的数据)，则这组数据的众数和方差分别是（）

A . 4，5 B . 4，3.2 C . 6，5 D . 4，16

查看解析收藏纠错

+选题

7. 一次数学测试，某小组5名同学的成绩统计如下：

组员	甲	乙	丙	丁	戊	平均成绩	中位数
得分	81	77	■	80	82	80	■

则被遮盖的两个数据依次是（）

A . 80，80 B . 81，80 C . 80，2 D . 81，2

查看解析收藏纠错

8. 某专卖店专销售某品牌运动鞋，店主对上一周中不同尺码的运动鞋销售情况统计如下：

尺码

40

41

42

43

44

平均每天销售数量/双

5

9

15

8

6

该店主决定本周进货时，增加些42码的运动鞋，影响该店主决策的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

查看解析收藏纠错

+选题
9. 若x，y，z的平均数是6，则5x＋3，5y－2，5z＋5的平均数是（）．

A . 6 B . 30 C . 33 D . 32

查看解析收藏纠错

+选题
10. 对于一组数据 3，3，2，3，6，3，10，3，6，3，2，下列结论正确的有（）．
①这组数据的众数是3；

②这组数据的众数与中位数的数值相等；

③这组数据的中位数与平均数的数值相等；

④这组数据的平均数与众数的数值相等．

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题

二、填空题

11. 已知一组数据从小到大排列为：-1，0，4，x，6，15，且这组数据的中位数是5，那么这组数据的众数是。

查看解析收藏纠错

+选题
12. 有一组数据如下：2，3，a，5，6，它们的平均数是4，则这组数据的方差是.

查看解析收藏纠错

+选题
13. 下图为甲、乙10次射击训练成绩的折线统计图。这些成绩的方差的大小关系是：S²_甲S²_乙。(选填“>”“=”“<”)

查看解析收藏纠错

+选题
14. 一组数据 $\text{[math]}$ 的平均数是2，方差是5，则 $\text{[math]}$ 的平均数和方差分别是、

查看解析收藏纠错

+选题
15. 已知一组数据-3，-2，1，3，6，x的中位数为1，则其方差为．

查看解析收藏纠错

+选题
16. 在学校举行的学生乐器演奏比赛中，八年级的10名学生成绩统计如图所示，则这 $\text{[math]}$ 名学生成绩的中位数是分．

查看解析收藏纠错

+选题
17. 某中学八年级通过网络开展了疫情为主题的演讲比赛，甲同学的各项得分成绩如下表所示：

项目

演讲内容

演讲技巧

仪表形象

甲

95

90

85

如果规定演讲内容、演讲技巧、仪表形象的三项成绩按6：3：1的比确定，那么甲的最终成绩为．

查看解析收藏纠错

+选题
18. 在从小到大排列的五个整数中，中位数是2，唯一的众数是4，则这五个数和的最大值是.

查看解析收藏纠错

+选题

三、解答题

19. 某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩，90分以上为优秀.甲、乙、丙三人的各项成绩如表（单位：分）：

	纸笔测试	实践能力	成长记录
甲	90	83	95
乙	96	82	94
丙	84	88	94

通过计算，确定学期总评成绩优秀的同学.

查看解析收藏纠错

20. 甲、乙两名射击运动员各进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9．乙的成绩如图所示（单位：环）

（1）分别计算甲、乙两人射击成绩的平均数；

（2）若要选拔一人参加比赛，应派哪一位？请说明理由．

查看解析收藏纠错

+选题
21. 在“爱满武汉”慈善捐款活动中，某学校团总支为了了解本校学生的捐款情况，抽取了50名学生的捐款数进行了统计，并绘制成统计图.

（1）这50名同学捐款的众数为元，中位数为元；

（2）求这50名同学捐款的平均数.

查看解析收藏纠错

+选题
22.
某商场统计了今年1～5月A，B两种品牌冰箱的销售情况，并将获得的数据绘制成折线统计图

（1）分别求该商场这段时间内A，B两种品牌冰箱月销售量的中位数和方差；

（2）根据计算结果，比较该商场1～5月这两种品牌冰箱月销售量的稳定性．

查看解析收藏纠错

+选题

23. 某校为提高学生的汉字书写能力，开展了“汉字听写”大赛．七、八年级学生参加比赛，为了解这两个年级参加比赛学生的成绩情况，从中各随机抽取10名学生的成绩，数据如下（单位：分）：

七年级 88 94 90 94 84 94 99 94 99 100

八年级 84 93 88 94 93 98 93 98 97 99

整理数据：按如下分数段整理数据并补全表格：

成绩x

人数年级

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

七年级

1

1

5

3

八年级

4

4

分析数据：补全下列表格中的统计量：

统计量

年级

平均数

中位数

众数

方差

七年级

93.6

94

24.2

八年级

93.7

93

20.4

得出结论：你认为哪个年级学生“汉字听写”大赛的成绩比较好？并说明理由．（至少从两个不同的角度说明推断的合理性）

查看解析收藏纠错

24. 福田区某中学开展“社会主义核心价值观”演讲比赛活动，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示．根据图中数据解决下列问题：

（1）九（1）班复赛成绩的中位数是分，九（2）班复赛成绩的众数是分；

（2）小明同学已经算出了九（1）班复赛的平均成绩 $\text{[math]}$ ，方差 $\text{[math]}$ ，请你求出九（2）班复赛的平均成绩 $\text{[math]}$ 和方差 $\text{[math]}$ ；

（3）根据（2）中计算结果，分析哪个班级的复赛成绩较好？

查看解析收藏纠错

+选题

25. 8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表（得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀）.

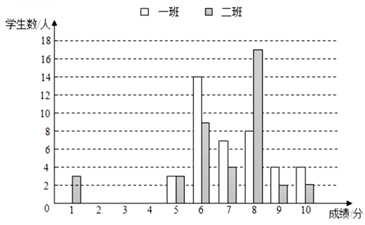
班级	平均分	方差	中位数	众数	合格率	优秀率
一班	$\text{[math]}$	2.11	7	$\text{[math]}$	92.5%	20%
二班	6.85	4.28	$\text{[math]}$	8	$\text{[math]}$	10%

根据图表信息，回答问题：

（1）直接写出表中a，b，c，d的值；

（2）用方差推断，班的成绩波动较大；用优秀率和合格率推断，班的阅读水平更好些；

（3）甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些。你认为谁的推断比较科学合理，更客观些，为什么？

查看解析收藏纠错

下载试卷答题卡下载在线测试收藏试卷分析试卷

相关试卷收起∨

试题篮