修改时间:2024-07-13 浏览次数:264 类型:月考试卷
|
组别 |
医务人员数分组 |
频数 |
频率 |
|
1 |
| 3 | b |
| 2 | | 10 | 0.33 |
| 3 | | a | 0.33 |
| 4 | | 4 | 0.14 |
| 5 | | 2 | 0.07 |
| 6 | | 1 | 0.03 |

根据以上信息回答下列问题:
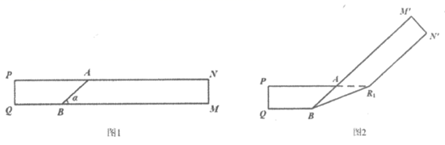
解决下面的问题:

①第二次折叠时,∠ =(用
的式子表示);
②第n次折叠时,∠ =(用
和n的式子表示).

试题篮