北京市北京中学明德分校2020-2021学年九年级上学期数学期中试卷

1. 一元二次方程 $\text{[math]}$ 的两根分别为 $\text{[math]}$ 则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 已知x₁ ， x₂是一元二次方程x²﹣4x+1=0的两个实数根，则x₁•x₂等于（）

A . ﹣4 B . ﹣1 C . 1 D . 4

查看解析收藏纠错

+选题
3. 已知关于x的一元二次方程x²﹣2x﹣k＝0有两个不相等的实数根，则实数k的取值范围是（　　）

A . k≥1 B . k＞1 C . k≥﹣1 D . k＞﹣1

查看解析收藏纠错

+选题
4. 若x₁ ， x₂是方程x²=4的两根，则x₁+x₂的值是（　　）

A . 0 B . 2 C . 4 D . 8

查看解析收藏纠错

+选题
5. 若 $\text{[math]}$ 为方程 $\text{[math]}$ 的一根， $\text{[math]}$ 为方程 $\text{[math]}$ 的一根，且 $\text{[math]}$ 都是正数，则 $\text{[math]}$ 为（）

A . 5 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 已知方程x²+bx+a＝0有一个根是﹣a（a≠0），则下列代数式的值恒为常数的是（　　）

A . ab B . $\text{[math]}$ C . a+b D . a﹣b

查看解析收藏纠错

+选题
7. 已知m是方程 $\text{[math]}$ 的一个根，则代数 $\text{[math]}$ 的值等于（）

A . -1 B . 0 C . 1 D . 2

查看解析收藏纠错

+选题
8. 如图，二次函数y=ax²+bx+c的图象与x轴两交点的横坐标分别为x₁ ， x₂ ，且x₁＜0＜x₂ ，则当ax²+bx+c≤0时，x的取值范围是（　　）

A . x₁＜x＜x₂ B . x₁≤x≤x₂ C . ﹣x₁≤x≤x₂ D . x≤x₁或x≥x₂

查看解析收藏纠错

+选题
9. 已知函数y=ax²+bx+c（a≠0）的图象如图，下列5个结论，其中正确的结论有（）
①abc＜0②3a+c＞0③4a+2b+c＜0④2a+b=0⑤b²＞4ac

A . 2 B . 3 C . 4 D . 5

查看解析收藏纠错

+选题
10. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E．若CE=4，DE=2，则AD的长是（）

A . 2 $\text{[math]}$ B . 6 C . 3 D . 6 $\text{[math]}$

查看解析收藏纠错

+选题

11. 方程x²－3＝0的根是．

查看解析收藏纠错

+选题
12. 已知关于x的方程x²+3x+a＝0有一个根为﹣2，则另一个根为．

查看解析收藏纠错

+选题
13. 已知关于x的一元二次方程x²+2x﹣（m﹣2）＝0有实数根，则m的取值范围是

查看解析收藏纠错

+选题
14. 关于x的方程 $\text{[math]}$ 是一元二次方程，则m；

查看解析收藏纠错

+选题
15. 下列关于x的方程中是一元二次方程的是（只填序号）．
⑴x²+1＝0；⑵ $\text{[math]}$ ；⑶ $\text{[math]}$ ；

⑷ $\text{[math]}$ ；⑸ $\text{[math]}$ ；⑹（x－2）（x－3）＝5．

查看解析收藏纠错

+选题
16. 甲卖橘子x千克与所获利润y（元）满足关系式 $\text{[math]}$ ，则当甲卖出千克橘子时，获得最大利润为元．

查看解析收藏纠错

+选题
17. 已知y与 $\text{[math]}$ 成正比例，且当 $\text{[math]}$ 时， $\text{[math]}$ ，则当 $\text{[math]}$ 时，x=．

查看解析收藏纠错

+选题
18. 如图，在Rt△AOB中，OA=OB= $\text{[math]}$ ，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为.

查看解析收藏纠错

+选题
19.
如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，∠B=70°，则∠DAC=.

查看解析收藏纠错

+选题
20. 如图，如果两个圆只有一个公共点，那么我们称这两个圆相切，这个公共点就叫做切点，当两圆相切时，如果其中一个圆（除切点外）在另一个圆的内部，叫做这两个圆内切；其中一个圆（除切点外）在另一个圆的外部，叫做这两个圆外切．如图所示：两圆的半径分别为R，r（R＞r），两圆的圆心之间的距离为d，若两个圆外切则d=R+r，若两个圆内切则d=R﹣r，已知两圆的半径分别为方程x²+mx+3=0的两个根，当两圆相切时，已知这两个圆的圆心之间的距离为4，则m的值为．

查看解析收藏纠错

+选题

21. 解方程：

（1） 2（x－3）²＝x²－9 ；

（2） $\text{[math]}$

查看解析收藏纠错

+选题
22. 已知关于x的一元二次方程（x-3）（x-2）=|m|．

（1）求证：对于任意实数m，方程总有两个不等的实数根；

（2）若方程的一个根是1，求m的值及方程的另一个根．

查看解析收藏纠错

+选题
23. 常德市工业走廊南起汉寿县太子庙镇，北玉桃源县盘塘镇创元工业园，在这一走廊内的工业企业2018年完成工业总产值440亿元，如果要在2020年达到743.6亿元，那么2018年到2020年的工业总产值年平均增长率是多少?《常德工业走廊建设发展规划纲要（草案）》确定2022年走廊内工业总产值要达到1200亿元，若继续保持上面的增长率，该目标是否可以完成?

查看解析收藏纠错

+选题

24. 蔬菜基地种植某种蔬菜，由市场行情分析知，1月份至6月份这种蔬菜的上市时间x（月份）与市场售价p（元/千克）的关系如下表：

上市时间x（月份）	1	2	3	4	5	6
市场售价p（元/千克）	10.5	9	7.5	6	4.5	3

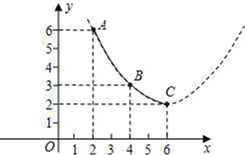
这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线的一段（如图）．

（1）写出上表中表示的市场售价p（元/千克）关于上市时间x（月份）的函数关系式；

（2）若图中抛物线过A，B，C点，写出抛物线对应的函数关系式；

（3）由以上信息分析，月份上市出售这种蔬菜每千克的收益最大，最大值为元（收益=市场售价一种植成本）．

查看解析收藏纠错

+选题

25. 如图，AB是圆O的直径，点C、D在圆O上，且AD平分∠CAB ．过点D作AC的垂线，与AC的延长线相交于E ，与AB的延长线相交于点F ．求证：EF与圆O相切．

查看解析收藏纠错

+选题
26.
已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．

（1）求证：BD是⊙O的切线；

（2）求证：CE²=EH•EA；

（3）若⊙O的半径为5，sinA= $\text{[math]}$ ，求BH的长。

查看解析收藏纠错

+选题

北京市北京中学明德分校2020-2021学年九年级上学期数学期中试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

北京市北京中学明德分校2020-2021学年九年级上学期数学期中试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨