修改时间:2021-05-20 浏览次数:1600 类型:中考真卷
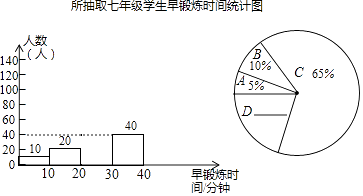
请你根据以上提供的信息,解答下列问题:
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
品种 项目 | 产量(斤/每棚) | 销售价(元/每斤) | 成本(元/每棚) |
香瓜 | 2000 | 12 | 8000 |
甜瓜 | 4500 | 3 | 5000 |
现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
根据以上情况,请你回答下列问题:
如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为;
如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
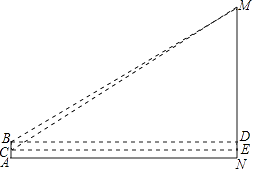
某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交 于点E,又测得DE=8m.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)

试题篮