江苏省镇江市2020年中考数学试卷

修改时间：2024-07-13 浏览次数：703 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 下列计算正确的是（）

A . a³+a³＝a⁶ B . （a³）²＝a⁶ C . a⁶÷a²＝a³ D . （ab）³＝ab³

查看解析收藏纠错

+选题
2. 如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体，这个几何体的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，它的图象不经过的象限是（）

A . 第一 B . 第二 C . 第三 D . 第四

查看解析收藏纠错

+选题
4. 如图，AB是半圆的直径，C、D是半圆上的两点，∠ADC＝106°，则∠CAB等于（）

A . 10° B . 14° C . 16° D . 26°

查看解析收藏纠错

+选题
5. 点P(m，n)在以y轴为对称轴的二次函数y＝x²+ax+4的图象上.则m﹣n的最大值等于（）

A . $\text{[math]}$ B . 4 C . ﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图①，AB＝5，射线AM∥BN，点C在射线BN上，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，点P，Q分别在射线AM、BN上，PQ∥AB.设AP＝x，QD＝y.若y关于x的函数图象（如图②）经过点E(9，2)，则cosB的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

7. $\text{[math]}$ 倒数是.

查看解析收藏纠错

+选题
8. 使 $\text{[math]}$ 有意义的x的取值范围是．

查看解析收藏纠错

+选题
9. 分解因式：9x²-1=．

查看解析收藏纠错

+选题
10. 2020年我国将完成脱贫攻坚目标任务.从2012年底到2019年底，我国贫困人口减少了93480000人，用科学记数法把93480000表示为.

查看解析收藏纠错

+选题
11. 一元二次方程x²﹣2x=0的解是．

查看解析收藏纠错

+选题
12. 一只不透明的袋子中装有5个红球和1个黄球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸出红球的概率等于.

查看解析收藏纠错

+选题
13. 圆锥底面圆半径为5，母线长为6，则圆锥侧面积等于.

查看解析收藏纠错

+选题
14. 点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）.这个图案绕点O至少旋转°后能与原来的图案互相重合.

查看解析收藏纠错

+选题
15. 根据数值转换机的示意图，输出的值为.

查看解析收藏纠错

+选题
16. 如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC的度数为°.

查看解析收藏纠错

+选题
17. 在从小到大排列的五个数x，3，6，8，12中再加入一个数，若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等，则x的值为.

查看解析收藏纠错

+选题
18. 如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A₁B₁C₁ ，点P、Q分别是AB、A₁C₁的中点，PQ的最小值等于.

查看解析收藏纠错

+选题

三、解答题

19.

（1）计算：4sin60°﹣ $\text{[math]}$ +( $\text{[math]}$ ﹣1)⁰；

（2）化简(x+1)÷(1+ $\text{[math]}$ ).

查看解析收藏纠错

+选题
20.

（1）解方程： $\text{[math]}$ ＝ $\text{[math]}$ +1；

（2）解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
21. 如图，AC是四边形ABCD的对角线，∠1＝∠B，点E、F分别在AB、BC上，BE＝CD，BF＝CA，连接EF.

（1）求证：∠D＝∠2；

（2）若EF∥AC，∠D＝78°，求∠BAC的度数.

查看解析收藏纠错

+选题

22. 教育部发布的义务教育质量监测结果报告显示，我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%.某校数学社团成员采用简单随机抽样的方法，抽取了本校八年级50名学生，对他们一周内平均每天的睡眠时间t（单位：小时）进行了调查，将数据整理后绘制成下表：

平均每天的睡眠时间分组	5≤t＜6	6≤t＜7	7≤t＜8	8≤t＜9	9小时及以上
频数	1	5	m	24	n

该样本中学生平均每天的睡眠时间达9小时及以上的比例高于全国的这项数据，达到了22%.

（1）求表格中n的值；

（2）该校八年级共400名学生，估计其中平均每天的睡眠时间在7≤t＜8这个范围内的人数是多少.

查看解析收藏纠错

+选题

23. 智慧的中国古代先民发明了抽象的符号来表达丰富的含义.例如，符号“ ”有刚毅的含义，符号“ ”有愉快的含义.符号中的“ ”表示“阴”，“ ”表示“阳”，类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中，每一行只有一个阴或一个阳，且出现阴、阳的可能性相同.

（1）所有这些三行符号共有种；

（2）若随机画一个这样的三行符号，求“画出含有一个阴和两个阳的三行符号”的概率.

查看解析收藏纠错

+选题
24. 如图，点E与树AB的根部点A、建筑物CD的底部点C在一条直线上，AC＝10m.小明站在点E处观测树顶B的仰角为30°，他从点E出发沿EC方向前进6m到点G时，观测树顶B的仰角为45°，此时恰好看不到建筑物CD的顶部D（H、B、D三点在一条直线上）.已知小明的眼睛离地面1.6m，求建筑物CD的高度（结果精确到0.1m）.（参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73.）

查看解析收藏纠错

+选题
25. 如图，正比例函数y＝kx（k≠0）的图象与反比例函数y＝﹣ $\text{[math]}$ 的图象交于点A(n，2)和点B.

（1） n＝，k＝；

（2）点C在y轴正半轴上.∠ACB＝90°，求点C的坐标；

（3）点P（m，0）在x轴上，∠APB为锐角，直接写出m的取值范围.

查看解析收藏纠错

+选题
26. 如图，▱ABCD中，∠ABC的平分线BO交边AD于点O，OD＝4，以点O为圆心，OD长为半径作⊙O，分别交边DA、DC于点M、N.点E在边BC上，OE交⊙O于点G，G为 $\text{[math]}$ 的中点.

（1）求证：四边形ABEO为菱形；

（2）已知cos∠ABC＝ $\text{[math]}$ ，连接AE，当AE与⊙O相切时，求AB的长.

查看解析收藏纠错

+选题
27.

（1）（算一算）

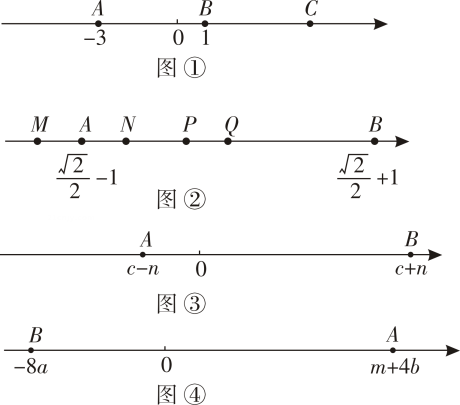
如图①，点A、B、C在数轴上，B为AC的中点，点A表示﹣3，点B表示1，则点C表示的数为，AC长等于；

（2）（找一找）
如图②，点M、N、P、Q中的一点是数轴的原点，点A、B分别表示实数 $\text{[math]}$ ﹣1、 $\text{[math]}$ +1，Q是AB的中点，则点是这个数轴的原点；

（3）（画一画）
如图③，点A、B分别表示实数c﹣n、c+n，在这个数轴上作出表示实数n的点E（要求：尺规作图，不写作法，保留作图痕迹）；

（4）（用一用）
学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测a个学生.凌老师提出了这样的问题：假设现在校门口有m个学生，每分钟又有b个学生到达校门口.如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校.在这些条件下，a、m、b会有怎样的数量关系呢？

爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数m+4b记作+(m+4b)，用点A表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数8a记作﹣8a，用点B表示.

①用圆规在小华画的数轴上分别画出表示+（m+2b）、﹣12a的点F、G，并写出+(m+2b)的实际意义；

②写出a、m的数量关系.

查看解析收藏纠错

+选题
28. 如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax²﹣2ax+c（a、c是常数，a＜0）的图象经过点M(﹣1，1)，交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点.

（1）当a＝﹣1时，求点N的坐标及 $\text{[math]}$ 的值；

（2）随着a的变化， $\text{[math]}$ 的值是否发生变化？请说明理由；

（3）如图②，E是x轴上位于点B右侧的点，BC＝2BE，DE交抛物线于点F.若FB＝FE，求此时的二次函数表达式.

查看解析收藏纠错

+选题

江苏省镇江市2020年中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨