海南省定安县2020年数学中考二模试卷

修改时间：2024-07-13 浏览次数：230 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 如果向西走30米记作－30米，那么向东走20米记作（）

A . －20米 B . +20米 C . －10米 D . +50米

查看解析收藏纠错

+选题
2. 下列运算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 地球上陆地的面积约为149 000 000平方千米，把数据149 000 000用科学记数法表示为 $\text{[math]}$ 米，其中 $\text{[math]}$ 等于（）

A . 6 B . 7 C . 8 D . 9

查看解析收藏纠错

+选题
4. 从不同方向看一只茶壶，你认为是俯视效果图的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 在函数y= $\text{[math]}$ 中，自变量x的取值范围是（）

A . x≤﹣3 B . x≥﹣3 C . x＜﹣3 D . x＞﹣3

查看解析收藏纠错

+选题
6. 在一个不透明的盒子中装有10个白球，若干个黄球，它们除颜色不同外，其余均相同.若从中随机摸出一个球，它是白球的概率为 $\text{[math]}$ ，则黄球的个数为（）

A . 4 B . 5 C . 6 D . 7

查看解析收藏纠错

+选题
7. 若一个正多边形的一个内角是144°，则这个多边形的边数为（）

A . 12 B . 11 C . 10 D . 9

查看解析收藏纠错

+选题
8. 如图， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 30° B . 45° C . 60° D . 120°

查看解析收藏纠错

+选题
9.
如图，△ABC的顶点都是正方形网格中的格点，则cos∠ABC等于（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 已知：如图，在△ABC中，∠ADE＝∠C，则下列等式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
11. 如图，直线l与x轴、y轴分别交于A、B两点，与反比例函数y＝ $\text{[math]}$ 的图象在第一象限相交于点C.若AB＝BC，△AOB的面积为3，则k的值为（）

A . 6 B . 9 C . 12 D . 18

查看解析收藏纠错

+选题
12. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 内切圆的半径是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题

13. 分解因式： $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 不等式组 $\text{[math]}$ 的解集为.

查看解析收藏纠错

+选题
15. 如图，矩形 $\text{[math]}$ 中，沿着直线 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 处， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是.

查看解析收藏纠错

+选题
16. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作圆与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则阴影部分的面积是 $\text{[math]}$ .

查看解析收藏纠错

+选题

三、解答题

17. 计算：

（1） $\text{[math]}$ ；

（2） $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 定安粽子有着“海南第一粽”之美称，定安粽分为两种，用糯米制作的又称糯米粽，用籼米制作的称籼米粽.小影购买6个糯米粽和4个籼米粽，共花费100元；小慧购买3个糯米粽和5个籼米粽，共花费71元.求糯米粽和籼米粽的单价分别是多少元？

查看解析收藏纠错

+选题

19. 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.

（1）确定调查方式时，甲同学说：“我到七年级（1）班去调查全体同学”；乙同学说：“放学时我到校门口随机调查部分同学”；丙同学说：“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.

（2）他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题：

类别	频数（人数）	频率
武术类		0.20
书画类	15	0.15
棋牌类	25	b
器乐类
合计	a	1.00

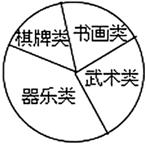
① _▲_， $\text{[math]}$ _▲_；

②在扇形统计图中，器乐类所对应扇形的圆心角是_▲_度；

③若该校七年级有学生460人，请你估计大约有多少学生参加武术类校本课程.

查看解析收藏纠错

+选题

20. 如图，某大楼的顶部有一块广告牌 $\text{[math]}$ ，小背在山坡的坡脚 $\text{[math]}$ 处测得广告牌底部的仰角为45°，沿坡面 $\text{[math]}$ 向上走到 $\text{[math]}$ 处测得广告牌顶部C的仰角为30°.已知山坡 $\text{[math]}$ 的坡度为 $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ 米.

此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.

（1）求点B距地面的高度 $\text{[math]}$ ；

（2）求广告牌 $\text{[math]}$ 的高度.（结果保留根号）

查看解析收藏纠错

+选题
21. 如图，在正方形 $\text{[math]}$ 中，E是边 $\text{[math]}$ 上的动点（与点A、D不重合），且 $\text{[math]}$ ， $\text{[math]}$ 于点G， $\text{[math]}$ 与 $\text{[math]}$ 的延长线交于点H，连接 $\text{[math]}$ 、 $\text{[math]}$ .

（1）求证：① $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ；② $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，在点E运动过程中，探究：
①线段 $\text{[math]}$ 的长度是否改变？若不变，求出这个定值；若改变，请说明理由；

②当 $\text{[math]}$ 为何值时， $\text{[math]}$ 为等腰直角三角形.

查看解析收藏纠错

+选题
22. 如图，抛物线 $\text{[math]}$ 与坐标轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 和点 $\text{[math]}$ ，连接 $\text{[math]}$ .

（1）求抛物线的解析式；

（2）如图，已知点P在线段 $\text{[math]}$ 的上方（不包括点B和点C），过P点作x轴的垂线交直线 $\text{[math]}$ 于点E，求线段 $\text{[math]}$ 的最大值；

（3）该抛物线上是否存在点P，使得 $\text{[math]}$ ？若存在，求点P的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题

海南省定安县2020年数学中考二模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨