修改时间:2016-07-04 浏览次数:534 类型:中考真卷
理解:数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
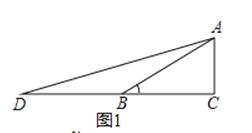
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC= . tanD=tan15°=
=
=2﹣
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)= . 假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
=
=2﹣
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
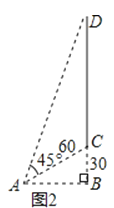
应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
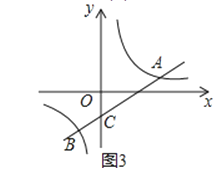
拓展:如图3,直线y=x﹣1与双曲线y=
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
试题篮