2017年辽宁省盘锦市中考数学一模试卷

1. ﹣2017的倒数是（）

A . 2017 B . ﹣2017 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . a²+a²=a⁴ B . （﹣b²）³=﹣b⁶ C . 2x•2x²=2x³ D . （m﹣n）²=m²﹣n²

查看解析收藏纠错

+选题
3. 由5个相同的立方体搭成的几何体如图所示，则它的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 某个密码锁的密码由三个数字组成，每个数字都是0﹣9这十个数字中的一个，只有当三个数字与所设定的密码及顺序完全相同时，才能将锁打开．如果仅忘记了锁设密码的最后那个数字，那么一次就能打开该密码的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 若关于x的一元二次方程（k﹣1）x²+4x+1=0有两个不相等的实数根，则k的取值范围是（）

A . k＜5 B . k＞5 C . k≤5，且k≠1 D . k＜5，且k≠1

查看解析收藏纠错

+选题
6. 随着居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查显示，截止2015年底某市汽车拥有量为16.9万辆．已知2013年底该市汽车拥有量为10万辆，设2013年底至2015年底该市汽车拥有量的年平均增长率为x，根据题意列方程得（）

A . 10（1+x）²=16.9 B . 10（1+2x）=16.9 C . 10（1﹣x）²=16.9 D . 10（1﹣2x）=16.9

查看解析收藏纠错

+选题
7. 不等式组 $\text{[math]}$ 的解集表示在数轴上，正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB= $\text{[math]}$ ，反比例函数y= $\text{[math]}$ 在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于（）

A . 60 B . 80 C . 30 D . 40

查看解析收藏纠错

+选题

10. 2016年第四季度全国网上商品零售额6310亿元，将6310亿元用科学记数法表示应为元．

查看解析收藏纠错

+选题
11. 分解因式：3m²﹣6mn+3n²=．

查看解析收藏纠错

+选题
12. 要使式子 $\text{[math]}$ 在实数范围内有意义，则实数x的取值范围是．

查看解析收藏纠错

+选题
13. 在△ABC中，AB=AC=10，cosB= $\text{[math]}$ ，如果圆O的半径为2 $\text{[math]}$ ，且经过点B、C，那么线段AO的长等于．

查看解析收藏纠错

+选题
14. 如图所示，平行四边形的两条对角线及过对角线交点的任意一条直线将平行四边形纸片分割成六个部分，现在平行四边形纸片上作随机扎针实验，针头扎在阴影区域内的概率为．

查看解析收藏纠错

+选题
15. 如图，从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A，B，C在圆周上，将剪下的扇形作为一个圆锥的侧面，则这个圆锥的底面圆的半径是cm．

查看解析收藏纠错

+选题
16. 如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF延长交AC于点E．若AB=10，BC=16，则线段EF的长为．

查看解析收藏纠错

+选题
17. 如图，二次函数y=ax²+bx+c（a≠0）的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x=2，且OA=OC，则下列结论：
①abc＞0；②9a+3b+c＜0；③c＞﹣1；
④关于x的方程ax²+bx+c=0（a≠0）有一个根为﹣ $\text{[math]}$
其中正确的结论个数有（填序号）

查看解析收藏纠错

+选题

18. 先化简，再求值：（ $\text{[math]}$ ﹣x+1）÷ $\text{[math]}$ ，其中x= $\text{[math]}$ ﹣2．

查看解析收藏纠错

+选题
19. 某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：
组号
分组
频数
一
6≤m＜7
2
二
7≤m＜8
7
三
8≤m＜9
a
四
9≤m≤10
2

（1）求a的值；

（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；

（3）将在第一组内的两名选手记为：A₁、A₂ ，在第四组内的两名选手记为：B₁、B₂ ，从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．

查看解析收藏纠错

+选题
20. 张家界市为了治理城市污水，需要铺设一段全长为300米的污水排放管道，铺设120米后，为了尽可能减少施工对城市交通所造成的影响，后来每天的工作量比原计划增加20%，结果共用了27天完成了这一任务，求原计划每天铺设管道多少米？

查看解析收藏纠错

+选题
21.
如图，小明在大楼45米高（即PH=45米，且PH⊥HC）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处得俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1： $\text{[math]}$ ．（点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上）

（1） ∠PBA的度数等于度；（直接填空）

（2）求A、B两点间的距离（结果精确到0.1米，参考数据： $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732）．

查看解析收藏纠错

+选题
22. 如图，AB是⊙O的直径，点C是⊙O上一点，AD和过点C的切线互相垂直，垂足为D，直线DC与AB的延长线相交于P．弦CE平分∠ACB，交直径AB于点F，连结BE．

（1）求证：AC平分∠DAB；

（2）探究线段PC，PF之间的大小关系，并加以证明；

（3）若tan∠CEB= $\text{[math]}$ ，BE=5 $\text{[math]}$ ，求AC、BC的长．

查看解析收藏纠错

+选题
23. “世界那么大，我想去看看”一句话红遍网络，骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场．顺风车行经营的A型车去年6月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售价比去年增加400元，若今年6月份与去年6月份卖出的A型车数量相同，则今年6月份A型车销售总额将比去年6月份销售总额增加25%．

（1）求今年6月份A型车每辆销售价多少元（用列方程的方法解答）；

（2）该车行计划7月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A、B两种型号车的进货和销售价格如表：

A型车
B型车
进货价格（元/辆）
1100
1400
销售价格（元/辆）
今年的销售价格
2400

查看解析收藏纠错

+选题
24. 在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C₁OD₁ ，旋转角为θ（0°＜θ＜90°），连接AC₁、BD₁ ， AC₁与BD₁交于点P．

（1）
如图1，若四边形ABCD是正方形．
①求证：△AOC₁≌△BOD₁ ．
②请直接写出AC₁ 与BD₁的位置关系．

（2）
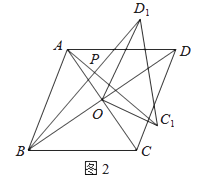
如图2，若四边形ABCD是菱形，AC=5，BD=7，设AC₁=kBD₁ ．判断AC₁与BD₁的位置关系，说明理由，并求出k的值．

（3）
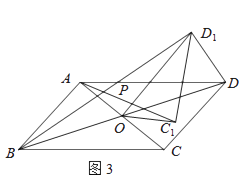
如图3，若四边形ABCD是平行四边形，AC=5，BD=10，连接DD₁ ，设AC₁=kBD₁ ．请直接写出k的值和AC₁²+（kDD₁）²的值．

查看解析收藏纠错

+选题
25.
如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4），以A为顶点的抛物线y=ax²+bx+c过点C，动点P从点A出发，以每秒 $\text{[math]}$ 个单位的速度沿线段AD向点D运动，运动时间为t秒，过点P作PE⊥x轴交抛物线于点M，交AC于点N．

（1）直接写出点A的坐标，并求出抛物线的解析式；

（2）当t为何值时，△ACM的面积最大？最大值为多少？

（3）点Q从点C出发，以每秒1个单位的速度沿线段CD向点D运动，当t为何值时，在线段PE上存在点H，使以C，Q，N，H为顶点的四边形为菱形？

查看解析收藏纠错

+选题

2017年辽宁省盘锦市中考数学一模试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

组号	分组	频数
一	6≤m＜7	2
二	7≤m＜8	7
三	8≤m＜9	a
四	9≤m≤10	2

	A型车	B型车
进货价格（元/辆）	1100	1400
销售价格（元/辆）	今年的销售价格	2400

2017年辽宁省盘锦市中考数学一模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨