修改时间:2024-07-12 浏览次数:445 类型:中考真卷
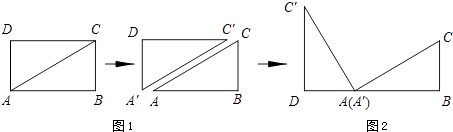
观察图2可知:与BC相等的线段是,∠CAC′=°.
拓展延伸
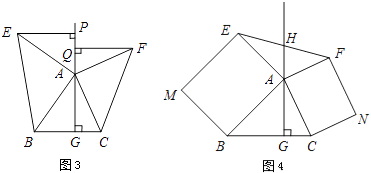
②如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.
如图,已知一次函数y=﹣x+7与正比例函数y= x的图象交于点A,且与x轴交于点B.
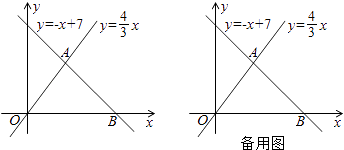
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
试题篮