2016-2017学年安徽省芜湖市芜湖县九年级上学期期中数学试卷

1. ﹣ $\text{[math]}$ 的倒数是（）

A . ﹣7 B . 7 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算中，正确的是（）

A . 2 $\text{[math]}$ +3 $\text{[math]}$ =5 $\text{[math]}$ B . ﹣a⁸÷a⁴=﹣a² C . （3a²）³=27a⁶ D . （a²﹣b）²=a⁴﹣b²

查看解析收藏纠错

+选题
4. 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 如图，在⊙O中，AB是直径，点C是 $\text{[math]}$ 的中点，点P是 $\text{[math]}$ 的中点，则∠PAB的度数（）

A . 30° B . 25° C . 22.5° D . 不能确定

查看解析收藏纠错

+选题
6. 如图，∠ABD=∠BDC=90°，∠A=∠CBD，AB=3，BD=2，则CD的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . 3

查看解析收藏纠错

+选题
7. 下列函数解析式中，一定为二次函数的是（　　）

A . y=3x﹣1 B . y=ax²+bx+c C . s=2t²﹣2t+1 D . y=x²+ $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中，点A在第一象限，AB⊥y轴于点B，函数 $\text{[math]}$ （k＞0，x＞0）的图象与线段AB交于点C，且AB=3BC．若△AOB的面积为12，则k的值为（）

A . 4 B . 6 C . 8 D . 12

查看解析收藏纠错

+选题

9. 分解因式：a²﹣3a=．

查看解析收藏纠错

+选题
10. 一个纳米粒子的直径是0.000 000 035米，用科学记数法表示为米．

查看解析收藏纠错

+选题
11. 如图，在△ABC中，AB＞AC，按以下步骤作图：分别以点B和点C为圆心，大于BC一半的长为半径作圆弧，两弧相交于点M和点N，作直线MN交AB于点D；连结CD．若AB=8，AC=3，则△ACD的周长为．

查看解析收藏纠错

+选题
12.
如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线y= $\text{[math]}$ x上一点，则点B与其对应点B′间的距离为．

查看解析收藏纠错

+选题
13. 如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为

查看解析收藏纠错

+选题
14. 如图，某抛物线的对称轴为直线x=2，点E是该抛物线顶点，抛物线与y轴交于点C，过点C作CD∥x轴，与抛物线交于点B，与对称轴交于点D，点A是对称轴上一点，连结AC、AB，若△ABC是等边三角形，则图中阴影部分图形的面积之和是．

查看解析收藏纠错

+选题

15. 先化简，再求值：（a+2）（a﹣2）+a（4﹣a），其中a=﹣ $\text{[math]}$ ．

查看解析收藏纠错

+选题
16. 在一个不透明的盒子里装有三个分别写有数字6，﹣2，7的小球，它们的形状、大小、质地完全相同，先从盒子里随机抽取一个小球，记下数字后放回盒子，摇匀后再随机取出一个小球，记下数字，请你用画树状图或列表的方法求两次取出小球上的数字和大于10的概率．

查看解析收藏纠错

+选题
17. 某工程队承接了3000米的修路任务，在修好600米后，引进了新设备，工作效率是原来的2倍，一共用30天完成了任务．求引进新设备前平均每天修路多少米？

查看解析收藏纠错

+选题
18. 已知二次函数y=ax²+k（a≠0），当x=2时，y=4；当x=﹣1时，y=﹣3，求这个二次函数解析式．

查看解析收藏纠错

+选题
19. “今天你光盘了吗？”这是国家倡导“厉行节约，反对浪费”以来的时尚流行语．某校团委随机抽取了部分学生，对他们进行了关于“光盘行动”所持态度的调查，并根据调查收集的数据绘制了如下两幅不完整的统计图：
根据上述信息，解答下列问题：

（1）抽取的学生人数为；

（2）将两幅统计图补充完整；

（3）请你估计该校1200名学生中对“光盘行动”持赞成态度的人数．

查看解析收藏纠错

+选题
20.
如图，某超市利用一个带斜坡的平台装卸货物，其纵断面ACFE如图所示． AE为台面，AC垂直于地面，AB表示平台前方的斜坡．斜坡的坡角∠ABC为45°，坡长AB为2m．为保障安全，又便于装卸货物，决定减小斜坡AB的坡角，AD 是改造后的斜坡（点D在直线BC上），坡角∠ADC为31°．求斜坡AD底端D与平台AC的距离CD．（结果精确到0.01m）[参考数据：sin31°=0.515，cos31°=0.857，tan31°=0.601， $\text{[math]}$ ≈1.414]．

查看解析收藏纠错

+选题
21. 如图，O为菱形ABCD对角线的交点，DE∥AC，CE∥BD．

（1）试判断四边形OCED的形状，并说明理由；

（2）若AC=6，BD=8，求线段OE的长．

查看解析收藏纠错

+选题
22. 甲、乙两支清雪队同时开始清理某路段积雪，一段时间后，乙队被调往别处，甲队又用了3小时完成了剩余的清雪任务，已知甲队每小时的清雪量保持不变，乙队每小时清雪50吨，甲、乙两队在此路段的清雪总量y（吨）与清雪时间x（时）之间的函数图象如图所示．

（1）乙队调离时，甲、乙两队已完成的清雪总量为吨；

（2）求此次任务的清雪总量m；

（3）求乙队调离后y与x之间的函数关系式．

查看解析收藏纠错

+选题
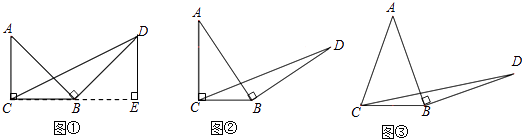
23. 问题原型：如图①，在等腰直角三角形ABC中，∠ACB=90°，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．过点D作△BCD的BC边上的高DE，
易证△ABC≌△BDE，从而得到△BCD的面积为 $\text{[math]}$ ．
初步探究：如图②，在Rt△ABC中，∠ACB=90°，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．用含a的代数式表示△BCD的面积，并说明理由．
简单应用：如图③，在等腰三角形ABC中，AB=AC，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．直接写出△BCD的面积．（用含a的代数式表示）

查看解析收藏纠错

+选题
24. 如图，菱形ABCD中，对角线AC ， BD相交于点O ，且AC=6cm，BD=8cm，动点P ， Q分别从点B ， D同时出发，运动速度均为1cm/s，点P沿B→C→D运动，到点D停止，点Q沿D→O→B运动，到点O停止1s后继续运动，到点B停止，连接AP ， AQ ， PQ ．设△APQ的面积为y（cm²）（这里规定：线段是面积0的几何图形），点P的运动时间为x（s）．

（1）填空：AB=cm，AB与CD之间的距离为 cm；

（2）当4≤x≤10时，求y与x之间的函数解析式；

（3）直接写出在整个运动过程中，使PQ与菱形ABCD一边平行的所有x的值．

查看解析收藏纠错

+选题

2016-2017学年安徽省芜湖市芜湖县九年级上学期期中数学试卷

一、选择题.

二、填空题：

三、解答题：

相关试卷收起∨

2016-2017学年安徽省芜湖市芜湖县九年级上学期期中数学试卷

一、选择题.

二、填空题：

三、解答题：

相关试卷 收起∨

相关试卷收起∨