修改时间:2024-07-13 浏览次数:1266 类型:中考真卷
如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.
若△ABC经γ(1,180°)变换后得△A1B1C1 , △A1B1C1经γ(2,180°)变换后得△A2B2C2 , △A2B2C2经γ(3,180°)变换后得△A3B3C3 , 依此类推……
△An-1B n-1C n-1经γ(n,180°)变换后得△AnBnCn , 则点A1的坐标是,点A2018的坐标是。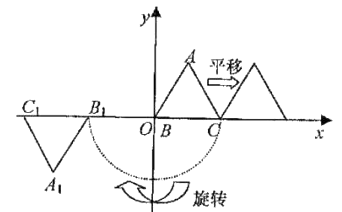

试题篮