题型:实践探究题 题类:真题 难易度:普通
山东省青岛市2018年中考数学试卷
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
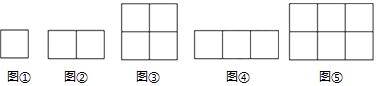
用若干木棒来搭建横长是m,纵长是n的矩形框架(m、n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条;
如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条;
如图③,当m=2,n=2时,横放木棒为2×(2+1))条,纵放木棒为(2+1)×2条,共需12条;如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条;
如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条.
问题(一):当m=4,n=2时,共需木棒条.
问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为条,
纵放的木棒为条.
探究二
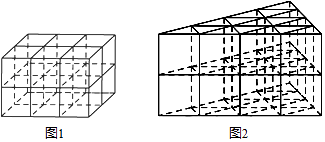
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m、n、s是正整数),需要木棒的条数.
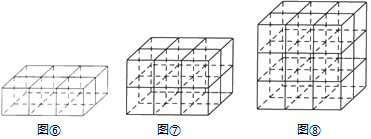
如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条;
如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条;
如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为条,竖放木棒条数为条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是.
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒条.
试题篮