如图①，

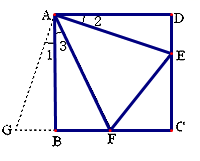
在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．

感悟解题方法，并完成下列填空：

将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：

AB=AD，BG=DE， ∠1=∠2，∠ABG=∠D=90°，

∴∠ABG+∠ABF=90°+90°=180°，

因此，点G，B，F在同一条直线上．

∵∠EAF=45°

∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．

∵∠1=∠2，  

∴∠1+∠3=45°．

即∠GAF=∠．

又AG=AE，AF=AF

∴△GAF≌．

∴=EF，故DE+BF=EF．

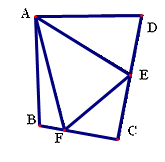
如图②，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF= ∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．

如图③，在四边形ABCD中，AB=AD，E，F分别为DC，BC上的点，满足∠EAF= ∠DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）

．