- 二一组卷

题型：综合题题类：模拟题难易度：困难

浙江省湖州市第四中学教育集团2019届数学第三次适应性考试试卷

定义：长宽比为 $\text{[math]}$ ：1（n为正整数）的矩形称为 $\text{[math]}$ 矩形.

下面，我们通过折叠的方式折出一个 $\text{[math]}$ 矩形，如图a所示.

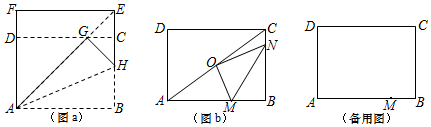
操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH.

操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD.则四边形ABCD为 $\text{[math]}$ 矩形.

（1）、证明：四边形ABCD为 $\text{[math]}$ 矩形；

（2）、点M是边AB上一动点.

①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN.求tan∠OMN的值；

②若AM=AD，点N在边BC上，当△DMN的周长最小时，求 $\text{[math]}$ 的值；

③连接CM，作BR⊥CM，垂足为R.若AB=2 $\text{[math]}$ ，则DR的最小值=.

举一反三

如图，已知直线a∥b∥c，直线d分别于直线a、b、c相交于点A、B、C，直线e分别与直线a、b、c相交于点D、E、F．若AB=2，BC=3，DE=3，则DF的长为{#blank#}1{#/blank#} ．

相关试卷