（苏科版）2023-2024学年九年级数学上册3.4 方差同步测试

1. 下列说法正确的是（）

A . 甲、乙两人跳远成绩的方差分别为s_甲²＝3，s_乙²＝4，说明乙的跳远成绩比甲稳定 B . 了解某市市民知晓“礼让行人”交通新规的情况，适合全面调查 C . 一组数据2，2，3，4的众数是2，中位数是2.5 D . 可能性是1%的事件在一次试验中一定不会发生

查看解析收藏纠错

+选题
2. 已知 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是按从小到大顺序排列的5个连续整数，若将这组数据变为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则这组新数据与原来相比（）

A . 平均数变大 B . 中位数变小 C . 极差变大 D . 方差变小

查看解析收藏纠错

+选题
3. 一组数据0、 $\text{[math]}$ 、2、 $\text{[math]}$ 、1的极差是（　　）

A . 2 B . 3 C . 4 D . 5

查看解析收藏纠错

+选题
4. 已知一组数据a、b、c、d的平均数是3，在这组数据后再添加数据3得到一组新数据a、b、c、d、3，则新数据与原数据相比，方差将（）

A . 不变 B . 变大 C . 变小 D . 不能确定

查看解析收藏纠错

+选题
5. 一组数据为7，9，9，11，若添加一个数据9，则发生变化的统计量是（）

A . 方差 B . 众数 C . 中位数 D . 平均数

查看解析收藏纠错

+选题
6. 下列判断正确的是（）

A . 北斗系统第五十五颗导航卫星发射前的零件检查，应选择抽样调查 B . 对于反比例函数y $\text{[math]}$ ， y随x增大而减小 C . 甲、乙两组学生身高的方差分别为 $\text{[math]}$ .则甲组学生的身高较整齐 D . 命题“既是矩形又是菱形的四边形是正方形”是真命题

查看解析收藏纠错

+选题
7. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 某校举行体操比赛，甲、乙两个班各选18名学生参加比赛，两个班参赛学生的平均身高都是1.72米，其方差分别是 $\text{[math]}$ ， $\text{[math]}$ ，则参赛学生身高比较整齐的班级是（）

A . 甲班 B . 乙班 C . 同样整齐 D . 无法确定

查看解析收藏纠错

+选题
9. 为了向建党一百周年献礼，我市中小学生开展了红色经典故事演讲比赛 $\text{[math]}$ 某参赛小组 $\text{[math]}$ 名同学的成绩 $\text{[math]}$ 单位：分 $\text{[math]}$ 分别为：85，82，86，82，83，92关于这组数据，下列说法错误的是（）

A . 众数是82 B . 中位数是84 C . 方差是84 D . 平均数是85

查看解析收藏纠错

+选题
10. 为考察甲、乙、丙、丁四个学生的学习情况，对这四名同学的四次测试成绩进行统计的平均数与方差为：
$\text{[math]}$ ＝ $\text{[math]}$ ＝85， $\text{[math]}$ ＝ $\text{[math]}$ ＝88， $\text{[math]}$ ＝ $\text{[math]}$ ＝0.5，S_乙²＝S_丙²＝4.5，则成绩又高又稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题

11. 如果一组数据3，5，x，6，8的众数为3，那么这组数据的方差为 .

查看解析收藏纠错

+选题
12. 在一次跳远训练中，甲、乙两人每人5次跳远的平均成绩都是 $\text{[math]}$ 米，方差分别是 $\text{[math]}$ （米 $\text{[math]}$ ）， $\text{[math]}$ （米 $\text{[math]}$ ），则在这次跳远训练中成绩比较稳定的是.

查看解析收藏纠错

+选题
13. 已知一组数据 $\text{[math]}$ 的极差为.

查看解析收藏纠错

+选题
14. 王大伯前几年承包了甲、乙两片荒山，各栽种了100棵杨梅树，成活98%，现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了四棵杨梅树上的杨梅，每棵的产量如图所示，由统计图提供的信息可知，杨梅产量较稳定的是.

查看解析收藏纠错

+选题
15. 农科院计划为某地选择合适的水果玉米种子，通过实验，甲、乙、丙、丁四种水果玉米种子每亩平均产量都是1500kg，方差分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则这四种水果玉米种子产量最稳定的是．（填“甲”“乙”“丙”“丁”）

查看解析收藏纠错

+选题

16. 两组数据：3，m，2n，5与m，6，n的平均数都是6，若将这两组数据合并为一组数据，求这组新数据的中位数、众数、方差．

查看解析收藏纠错

+选题

17. 某中学形展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．

（1）根据图示填写下表：

班级	平均数（分）	中位数（分）	众数（分）
九（1）		85
九（2）	85		100

（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；

（3）计算两班复赛成绩的方差．

查看解析收藏纠错

+选题

18. 学校为了让同学们走向操场、积极参加体育锻炼，启动了“学生阳光体育运动”，张明和李亮在体育运动中报名参加了百米训练小组，在近几次百米训练中，教练对他们两人的测试成绩进行了统计和分析，请根据图表中的信息解答以下问题：

平均数
中位数
方差
张明
$\text{[math]}$
$\text{[math]}$
李亮
$\text{[math]}$

（1）李亮成绩的中位数为：秒；

（2）计算张明成绩的平均数和李亮成绩的方差；

（3）现在从张明和李亮中选择一名成绩比较稳定的去参加比赛，若你是他们的教练，应该选择谁？请说明理由．

查看解析收藏纠错

+选题
19. 甲、乙两人参加射箭比赛，两人各射了5箭，他们的成绩（单位：环）统计如下表.

第1箭
第2箭
第3箭
第4箭
第5箭
甲成绩
9
4
7
4
6
乙成绩
7
5
6
5
7

（1）分别计算甲、乙两人射箭比赛的平均成绩；

（2）你认为哪个人的射箭成绩比较稳定?为什么?

查看解析收藏纠错

+选题

20. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8

（1）根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；

（2）分别计算甲、乙六次测试成绩的方差；你认为推荐谁参加全国比赛更合适，请说明理由.

查看解析收藏纠错

+选题
21. 为了提高农副产品的国际竞争力，我国一些行业协会对农副产品的规格进行了划分．某外贸公司要出口一批规格为75g的鸡腿，现有两个厂家提供货源，它们的价格相同，鸡腿的品质相近，质检员分别从两厂的产品中抽样调查了20只鸡腿，它们的质量（单位：g）如下：
甲厂：76，74，74，76，73，76，76，77，78，74，76，70，76，76，73，70，77，79，78，71；
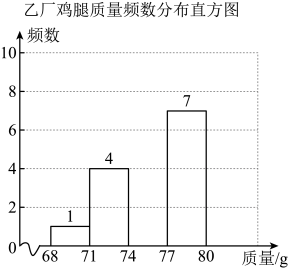
乙厂：75，76，77，77，78，77，76，71，74，75，79，71，72，74，73，74，70，79，75，77．
甲厂鸡腿质量频数统计表
质量x（g）
频数
频率
68≤x＜71
2
0.1
71≤x＜74
3
0.15
74≤x＜77
10
a
77≤x＜80
5
0.25
合计
20
1
分析上述数据，得到下表：
统计量厂家
平均数
中位数
众数
方差
甲厂
75
76
b
6.3
乙厂
75
c
77
6.6
请你根据图表中的信息完成下列问题：

（1） a＝；b＝；c＝；

（2）补全频数分布直方图；

（3）如果只考虑出口鸡腿规格，请结合表中的某个统计量，为外贸公司选购鸡腿提供参考建议；

（4）某外贸公司从甲厂采购了20000只鸡腿，并将质量（单位：g）在71≤x＜77的鸡腿加工成优等品，请估计可以加工成优等品的鸡腿有多少只？

查看解析收藏纠错

+选题
22. 某中学八年级甲、乙两班分别选5名同学参加“防疫宣传”演讲比赛，其预赛成绩 $\text{[math]}$ 单位：分 $\text{[math]}$ 如图所示：
根据以上信息，解答下列问题：

（1）求出表中的 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ；

平均数
中位数
众数
方差
甲班
8.5
$\text{[math]}$
8.5
$\text{[math]}$
乙班
$\text{[math]}$
8
$\text{[math]}$
1.6

（2）请你任选一组统计量描述两个班的成绩水平？

（3）乙班小明说：“我的成绩在我们班是中等水平”，你知道他是几号选手吗？

查看解析收藏纠错

+选题
23. 某中学八年级甲、乙两班分别选5名同学参加“防疫宣传”演讲比赛，其预赛成绩（单位：分）如图所示：

根据以上信息，解答下列问题

（1）求出表中的a、b、c、d

平均数
中位数
众数
方差
甲班
8.5
b
8.5
d
乙班
a
8
c
1.6

（2）请你任选一组统计量描述两个班的成绩水平

（3）乙班小明说：“我的成绩在我们班是中等水平”，你知道他是几号选手吗?

查看解析收藏纠错

+选题

（苏科版）2023-2024学年九年级数学上册3.4 方差同步测试

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

	平均数	中位数	方差
张明		$\text{[math]}$	$\text{[math]}$
李亮	$\text{[math]}$

	第1箭	第2箭	第3箭	第4箭	第5箭
甲成绩	9	4	7	4	6
乙成绩	7	5	6	5	7

	第一次	第二次	第三次	第四次	第五次	第六次
甲	10	8	9	8	10	9
乙	10	7	10	10	9	8

质量x（g）	频数	频率
68≤x＜71	2	0.1
71≤x＜74	3	0.15
74≤x＜77	10	a
77≤x＜80	5	0.25
合计	20	1

统计量厂家	平均数	中位数	众数	方差
甲厂	75	76	b	6.3
乙厂	75	c	77	6.6

	平均数	中位数	众数	方差
甲班	8.5	b	8.5	d
乙班	a	8	c	1.6

（苏科版）2023-2024学年九年级数学上册3.4 方差 同步测试

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

（苏科版）2023-2024学年九年级数学上册3.4 方差同步测试

相关试卷收起∨