2023年中考数学真题分类汇编（全国版）：数据收集与处理（2）

修改时间：2023-07-27 浏览次数：100 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 空气的成分（除去水汽、杂质等）是：氮气约占78%，氧气约占21%，其他微量气体约占1%．要反映上述信息，宜采用的统计图是（）

A . 条形统计图 B . 折线统计图 C . 扇形统计图 D . 频数分布直方图

查看解析收藏纠错

+选题
2. 阅读背景素材，完成下面小题.
某校计划组织研学活动，现有四个地点可供选择：南麂岛、百丈漈、楠溪江、雁荡山.

（1）若从中随机选择一个地点，则选中“南麂岛”或“百丈漈”的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

（2）为了解学生想法，校方进行问卷调查（每人选一个地点），并绘制成如图所示统计图.已知选择雁荡山的有270人，那么选择楠溪江的有（）

A . 90人 B . 180人 C . 270人 D . 360人

查看解析收藏纠错

+选题
3. 以下调查中，适合全面调查的是（）．

A . 了解全国中学生的视力情况 B . 检测“神舟十六号”飞船的零部件 C . 检测台州的城市空气质量 D . 调查某池塘中现有鱼的数量

查看解析收藏纠错

+选题
4. 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼．小亮记录了自己一周内每天校外锻炼的时间（单位：分钟），并制作了如图所示的统计图．

根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（）

A . 平均数为70分钟 B . 众数为67分钟 C . 中位数为67分钟 D . 方差为0

查看解析收藏纠错

+选题

5. 据统计，数学家群体是一个长寿群体，某研究小组随机抽取了收录约 $\text{[math]}$ 位数学家的《数学家传略辞典》中部分 $\text{[math]}$ 岁及以上的长寿数学家的年龄为样本，对数据进行整理与分析，统计图表（部分数据）如下，下列结论错误的是（）

年龄范围（岁）	人数（人）
$\text{[math]}$	25
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$	11
$\text{[math]}$	10
$\text{[math]}$	$\text{[math]}$

A . 该小组共统计了100名数学家的年龄 B . 统计表中 $\text{[math]}$ 的值为5 C . 长寿数学家年龄在 $\text{[math]}$ 岁的人数最多 D . 《数学家传略辞典》中收录的数学家年龄在 $\text{[math]}$ 岁的人数估计有110人

查看解析收藏纠错

+选题

6. 乐山是一座著名的旅游城市，有着丰富的文旅资源．某校准备组织初一年级500名学生进行研学旅行活动，政教处周老师随机抽取了其中50名同学进行研学目的地意向调查，并将调查结果制成如下统计图，如图所示估计初一年级愿意去“沫若故居”的学生人数为（）

A . 100 B . 150 C . 200 D . 400

查看解析收藏纠错

+选题

二、填空题

7. 某校为了解学生对A，B，C，D四类运动的参与情况，随机调查了本校80名学生，让他们从中选择参与最多的一类，得到对应的人数分别是30，20，18，12．若该校有800名学生，则估计有人参与A类运动最多．

查看解析收藏纠错

+选题
8. 如图，条形图描述了某车间工人日加工零件数的情况．这些工人日加工零件数的中位数是．

查看解析收藏纠错

+选题

三、综合题

9. 为了解学生完成书面作业所用时间的情况，进一步优化作业管理，某中学从全校学生中随机抽取部分学生，对他们一周平均每天完成书面作业的时间t（单位：分钟）进行调查.将调查数据进行整理后分为五组：A组“ $\text{[math]}$ ”；B组“ $\text{[math]}$ ”；C组“ $\text{[math]}$ ”；D组“ $\text{[math]}$ ”；E组“ $\text{[math]}$ ”.现将调查结果绘制成如下两幅不完整的统计图.

根据以上信息，解答下列问题：

（1）这次调查的样本容量是 ▲ ，请补全条形统计图；

（2）在扇形统计图中，A组对应的圆心角的度数是°，本次调查数据的中位数落在组内；

（3）若该中学有2000名学生，请你估计该中学一周平均每天完成书面作业不超过90分钟的学生有多少人？

查看解析收藏纠错

+选题

10. 某校数学兴趣小组的同学们从“校园农场“中随机抽取了 $\text{[math]}$ 棵西红柿植株，并统计了每棵植株上小西红柿的个数 $\text{[math]}$ 其数据如下： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 通过对以上数据的分析整理，绘制了统计图表：

分组	频数	组内小西红柿的总个数
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

根据以上信息，解答下列问题：

（1）补全频数分布直方图：这 $\text{[math]}$ 个数据的众数是 ▲ ；

（2）求这 $\text{[math]}$ 个数据的平均数；

（3） “校园农场“中共有 $\text{[math]}$ 棵这种西红柿植株，请估计这 $\text{[math]}$ 棵西红柿植株上小西缸柿的总个数．

查看解析收藏纠错

+选题

11. 首届楚文化节在荆州举办前，主办方为使参与服务的志愿者队伍整齐，随机抽取了部分志愿者，对其身高进行调查，将身高（单位：cm）数据分A，B，C，D，E五组制成了如下的统计图表（不完整）．

组别	身高分组	人数
A	155≤x＜160	3
B	160≤x＜165	2
C	165≤x＜170	m
D	170≤x＜175	5
E	175≤x＜180	4

根据以上信息回答：

（1）这次被调查身高的志愿者有人，表中的 $\text{[math]}$ ，扇形统计图中α的度数是；

（2）若E组的4人中，男女各有2人，以抽签方式从中随机抽取两人担任组长．请列表或画树状图，求刚好抽中两名女志愿者的概率．

查看解析收藏纠错

+选题

12. 某中学把开展课外经典阅读活动作为一项引领学生明是非、知荣辱、立志向、修言行的德育举措．为了调查活动开展情况，需要了解全校2000名学生一周的课外经典阅读时间．从本校学生中随机抽取100名进行调查，将调查的一周课外经典阅读的平均时间 $\text{[math]}$ 分为5组：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ，并将调查结果用如图所示的统计图描述．

根据以上信息，解答下列问题：

（1）本次调查中，一周课外经典阅读的平均时间的众数和中位数分别落在第组和第组（填序号）；一周课外经典阅读的平均时间达到4小时的学生人数占被调查人数的百分比为；估计全校一周课外经典阅读的平均时间达到4小时的学生有人；

（2）若把各组阅读时间的下限与上限的中间值近似看作该组的平均阅读时间，估计这100名学生一周课外经典阅读的平均时间是多少？

（3）若把一周课外经典阅读的平均时间达到4小时的人数百分比超过 $\text{[math]}$ ，作为衡量此次开展活动成功的标准，请你评价此次活动，并提出合理化的建议．

查看解析收藏纠错

+选题
13. 某校计划组织学生外出开展研学活动，在选择研学活动地点时，随机抽取了部分学生进行调查，要求被调查的学生从A、B、C、D、E五个研学活动地点中选择自己最喜欢的一个．根据调查结果，编制了如下两幅不完整的统计图．

（1）请把图1中缺失的数据，图形补充完整；

（2）请计算图2中研学活动地点C所在扇形的圆心角的度数；

（3）若该校共有1200名学生，请估计最喜欢去D地研学的学生人数．

查看解析收藏纠错

+选题
14. 中共中央办公厅、国务院办公厅印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》中，对学生每天的作业时间提出明确要求：“初中书面作业平均完成时间不超过90分钟”．为了更好地落实文件精神，某县对辖区内部分初中学生就“每天完成书面作业的时间”进行了随机调查，为便于统计学生每天完成书面作业的时间（用t表示，单位h）状况设置了如下四个选项，分别为A： $\text{[math]}$ ， B： $\text{[math]}$ ， C： $\text{[math]}$ ， D： $\text{[math]}$ ，并根据调查结果绘制了如下两幅不完整的统计图．

请根据以上提供的信息解答下列问题：

（1）此次调查，选项A中的学生人数是多少？

（2）在扇形统计图中，选项D所对应的扇形圆心角的大小为多少？

（3）如果该县有15000名初中学生，那么请估算该县“每天完成书面作业的时间不超过90分钟”的初中学生约有多少人？

（4）请回答你每天完成书面作业的时间属于哪个选项，并对老师的书面作业布置提出合理化建议．

查看解析收藏纠错

+选题
15. 某市对九年级学生进行“综合素质”评价，评价的结果为A（优）、B（良好）、C（合格）、D（不合格）四个等级．现从中随机抽测了若干名学生的“综合素质”等级作为样本进行数据处理，并作出了如下频数分布图和如图（八）所示的条形统计图（不完整）．请根据图表中的信息回答下列问题．
等级
频数
频率
A
a
0.2
B
1600
b
C
1400
0.35
D
200
0.05

（1）求频数分布表中a，b的值．

（2）补全条形统计图．

（3）该市九年级学生约 $\text{[math]}$ 人，试估计该市有多少名九年级学生可以评为“A”级．

查看解析收藏纠错

+选题

16. 为增强学生的社会实践能力，促进学生全面发展，某校计划建立小记者站，有20名学生报名参加选拔．报名的学生需参加采访、写作、摄影三项测试，每项测试均由七位评委打分（满分100分），取平均分作为该项的测试成绩，再将采访、写作、摄影三项的测试成绩按 $\text{[math]}$ 的比例计算出每人的总评成绩．

小悦、小涵的三项测试成绩和总评成绩如下表，这20名学生的总评成绩频数直方图（每组含最小值，不含最大值）如下图

选手	测试成绩/分			总评成绩/分
选手	采访	写作	摄影	总评成绩/分
小悦	83	72	80	78
小涵	86	84	▲	▲

（1）在摄影测试中，七位评委给小涵打出的分数如下：67，72，68，69，74，69，71．这组数据的中位数是分，众数是分，平均数是分；

（2）请你计算小涵的总评成绩；

（3）学校决定根据总评成绩择优选拔12名小记者．试分析小悦、小涵能否入选，并说明理由．

查看解析收藏纠错

+选题

17. 为进一步落实“德、智、体、美、劳”五育并举工作，某校开展以“文化、科技、体育、艺术、劳动”为主题的活动，其中体育活动有“一分钟跳绳”比赛项目，为了解学生“一分钟跳绳”的能力，体育老师随机抽取部分学生进行测试并将测试成绩作为样本，绘制出如图所示的频数分布直方图（从左到右依次为第一到第六小组，每小组含最小值，不含最大值）和扇形统计图，请根据统计图中提供的信息解答下列问题：

（1）求第四小组的频数，并补全频数分布直方图；

（2）若“一分钟跳绳”不低于160次的成绩为优秀，本校学生共有1260人，请估计该校学生“一分钟跳绳”成绩为优秀的人数；

（3）若“一分钟跳绳”不低于180次的成绩为满分，经测试某班恰有3名男生1名女生成绩为满分，现要从这4人中随机抽取2人去参加学校组织的“一分钟跳绳”比赛，请用画树状图或列表的方法，求所选2人都是男生的概率．

查看解析收藏纠错

+选题
18. 某校为落实国家“双减”政策，丰富课后服务内容，为学生开设五类社团活动（要求每人必须参加且只参加一类活动）：A．音乐社团；B．体育社团；C．美术社团；D．文学社团；E．电脑编程社团，该校为了解学生对这五类社团活动的喜爱情况，随机抽取部分学生进行了调查统计，并根据调查结果，绘制了如图所示的两幅不完整的统计图．

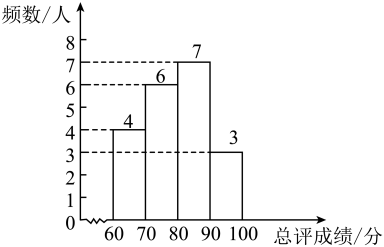
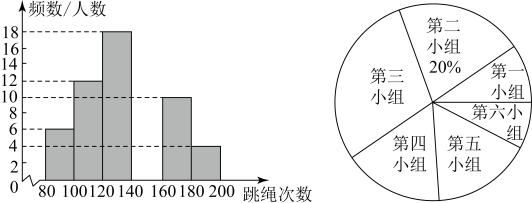
根据图中信息，解答下列问题：

（1）此次调查一共随机抽取了名学生，补全条形统计图（要求在条形图上方注明人数）；

（2）扇形统计图中圆心角 $\text{[math]}$ 度；

（3）现从“文学社团”里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛，请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率．

查看解析收藏纠错

+选题
19. 市体育局对甲、乙两运动队的某体育项目进行测试，两队人数相等，测试后统计队员的成绩分别为：7分、8分、9分、10分（满分为10分）．依据测试成绩绘制了如图所示尚不完整的统计图表：
甲队成绩统计表

成绩

7分

8分

9分

10分

人数

0

1

m

7

请根据图表信息解答下列问题：

（1）填空： $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ；

（2）补齐乙队成绩条形统计图；

（3） ①甲队成绩中位数为 ▲ ，乙队成绩的中位数为 ▲ ；
②分别计算甲、乙两队成绩的平均数，并从中位数和平均数的角度分析哪个运动队的成绩较好．

查看解析收藏纠错

+选题
20. 中学生心理健康受到社会的广泛关注，某校开展心理健康教育专题讲座，就学生对心理健康知识的了解程度，采用随机抽样调查的方式，根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．

根据图中信息回答下列问题：

（1）接受问卷调查的学生共有人，条形统计图中m的值为，扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为；

（2）若该校共有学生800人，根据上述调查结果，可以估计出该校学生中对心理健康知识“不了解”的总人数为人；

（3）若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛，请用列表或画树状图的方法，求恰好抽到2名女生的概率．

查看解析收藏纠错

+选题

21. 某校为了解学生参加家务劳动的情况，随机抽取了部分学生在某个休息日做家务的劳动时间 $\text{[math]}$ （单位： $\text{[math]}$ ）作为样本，将收集的数据整理后分为 $\text{[math]}$ 五个组别，其中A组的数据分别为：0.5，0.4，0.4，0.4，0.3，绘制成如下不完整的统计图表．

各组劳动时间的频数分布表

组别	时间 $\text{[math]}$	频数
$\text{[math]}$	$\text{[math]}$	5
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	20
$\text{[math]}$	$\text{[math]}$	15
$\text{[math]}$	$\text{[math]}$	8

各组劳动时间的扇形统计图

请根据以上信息解答下列问题．

（1） A组数据的众数是；

（2）本次调查的样本容量是，B组所在扇形的圆心角的大小是；

（3）若该校有 $\text{[math]}$ 名学生，估计该校学生劳动时间超过 $\text{[math]}$ 的人数．

查看解析收藏纠错

+选题

22. “阅读新时代，书香满宜昌”．在“全民阅读月”活动中，某校提供了四类适合学生阅读的书籍：A文学类，B科幻类，C漫画类，D数理类．为了解学生阅读兴趣，学校随机抽取了部分学生进行调查（每位学生仅选一类）．根据收集到的数据，整理后得到下列不完整的图表：

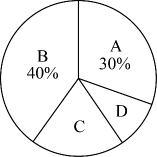
书籍类别学生人数

A文学类 24

B科幻类 m

C漫画类 16

D数理类 8

（1）本次抽查的学生人数是，统计表中的 $\text{[math]}$ ；

（2）在扇形统计图中，“C漫画类”对应的圆心角的度数是；

（3）若该校共有1200名学生，请你估计该校学生选择“D数理类”书籍的学生人数；

（4）学校决定成立“文学”“科幻”“漫画”“数理”四个阅读社团．若小文、小明随机选取四个社团中的一个，请利用列表或画树状图的方法，求他们选择同一社团的概率．

查看解析收藏纠错

+选题
23. 跳绳是某校体育活动的特色项目．体育组为了了解七年级学生1分钟跳绳次数情况，随机抽取20名七年级学生进行1分钟跳绳测试（单位：次），数据如下：
100　　110　　114　　114　　120　　122　　122　　131　　144　　148
152　　155　　156　　165　　165　　165　　165　　174　　188　　190
对这组数据进行整理和分析，结果如下：
平均数
众数
中位数
145
$\text{[math]}$
$\text{[math]}$
请根据以上信息解答下列问题：

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ；

（2）学校规定1分钟跳绳165次及以上为优秀，请你估计七年级240名学生中，约有多少名学生能达到优秀？

（3）某同学1分钟跳绳152次，请推测该同学的1分钟跳绳次数是否超过年级一半的学生？说明理由．

查看解析收藏纠错

+选题
24. 《义务教育课程方案》和《义务教育劳动课程标准（2022年版）》正式发布，劳动课正式成为中小学的一门独立课程，日常生活劳动设定四个任务群：A清洁与卫生，B整理与收纳，C家用器具使用与维护，D烹饪与营养．学校为了较好地开设课程，对学生最喜欢的任务群进行了调查，并将调查结果绘制成以下两幅不完整的统计图．

请根据统计图解答下列问题：

（1）本次调查中，一共调查了名学生，其中选择“C家用器具使用与维护”的女生有名，“D烹饪与营养”的男生有名．

（2）补全上面的条形统计图和扇形统计图；

（3）学校想从选择“C家用器具使用与维护”的学生中随机选取两名学生作为“家居博览会”的志愿者，请用画树状图或列表法求出所选的学生恰好是一名男生和一名女生的概率．

查看解析收藏纠错

+选题
25. 2023年3月27日是第28个全国中小学生安全教育日，为提高学生安全防范意识和自我防护能力，某学校举行了校园安全知识竞赛活动．现从八、九年级中各随机抽取15名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，80分及以上为优秀，共分成四组，A： $\text{[math]}$ ；B： $\text{[math]}$ ；C： $\text{[math]}$ ；D： $\text{[math]}$ ），并给出下面部分信息：
八年级抽取的学生竞赛成绩在C组中的数据为：84，84，88．
九年级抽取的学生竞赛成绩为：68，77，75，100，80，100，82，86，95，91，100，86，84，94，87．

八、九年级抽取的学生竞赛成绩统计表
年级
平均数
中位数
众数
优秀率
八
87
a
98
$\text{[math]}$
九
87
86
b
c
根据以上信息，解答下列问题：

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

（2）该校八、九年级共500人参加了此次竞赛活动，请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数．

查看解析收藏纠错

+选题
26. “基础学科拔尖学生培养试验计划”简称“珠峰计划”，是国家为回应“钱学森之间”而推出的一项人才培养计划，旨在培养中国自己的杰出人才．已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五所大学设有数学学科拔尖学生培养基地，并开设了暑期夏令营活动，参加活动的每名中学生只能选择其中一所大学．某市为了解中学生的参与情况，随机抽取部分学生进行调查，并将统计数据整理后，绘制了如下不完整的条形统计图和扇形统计图．

（1）请将条形统计图补充完整；

（2）在扇形统计图中， $\text{[math]}$ 所在的扇形的圆心角的度数为；若该市有 $\text{[math]}$ 中学生参加本次活动，则选择 $\text{[math]}$ 大学的大约有人；

（3）甲、乙两位同学计划从 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三所大学中任选一所学校参加夏令营活动，请利用树状图或表格求两人恰好选取同一所大学的概率．

查看解析收藏纠错

+选题
27. 某校八年级共有200名学生，为了解八年级学生地理学科的学习情况，从中随机抽取40名学生的八年级上、下两个学期期末地理成绩进行整理和分析（两次测试试卷满分均为35分，难度系数相同；成绩用 $\text{[math]}$ 表示，分成6个等级： $\text{[math]}$ ． $\text{[math]}$ ； $\text{[math]}$ ． $\text{[math]}$ ； $\text{[math]}$ ． $\text{[math]}$ ； $\text{[math]}$ ． $\text{[math]}$ ； $\text{[math]}$ ． $\text{[math]}$ ； $\text{[math]}$ ． $\text{[math]}$ ）．下面给出了部分信息：
a．八年级学生上、下两个学期期末地理成绩的统计图如下：
b．八年级学生上学期期末地理成绩在 $\text{[math]}$ ． $\text{[math]}$ 这一组的成绩是：
15，15，15，15，15，16，16，16，18，18
c．八年级学生上、下两个学期期末地理成绩的平均数、众数、中位数如下：
学期
平均数
众数
中位数
八年级上学期
$\text{[math]}$
15
$\text{[math]}$
八年级下学期
$\text{[math]}$
19
$\text{[math]}$
根据以上信息，回答下列问题：

（1）填空： $\text{[math]}$ ；

（2）若 $\text{[math]}$ 为优秀，则这200名学生八年级下学期期末地理成绩达到优秀的约有人；

（3）你认为该校八年级学生的期末地理成绩下学期比上学期有没有提高？请说明理由．

查看解析收藏纠错

+选题
28. 近年，“青少年视力健康”受到社会的广泛关注．某校综合实践小组为了解该校学生的视力健康状况，从全校学生中随机抽取部分学生进行视力调查．根据调查结果和视力有关标准，绘制了两幅不完整的统计图．请根据图中信息解答下列问题：

（1）所抽取的学生人数为；

（2）补全条形统计图，并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数；

（3）该校共有学生 $\text{[math]}$ 人，请估计该校学生中近视程度为“轻度近视”的人数．

查看解析收藏纠错

+选题

书籍类别	学生人数
A文学类	24
B科幻类	m
C漫画类	16
D数理类	8

年级	平均数	中位数	众数	优秀率
八	87	a	98	$\text{[math]}$
九	87	86	b	c

学期	平均数	众数	中位数
八年级上学期	$\text{[math]}$	15	$\text{[math]}$
八年级下学期	$\text{[math]}$	19	$\text{[math]}$

等级	频数	频率
A	a	0.2
B	1600	b
C	1400	0.35
D	200	0.05

成绩	7分	8分	9分	10分
人数	0	1	m	7

2023年中考数学真题分类汇编（全国版）：数据收集与处理（2）

一、选择题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨