修改时间:2024-07-13 浏览次数:273 类型:中考真卷
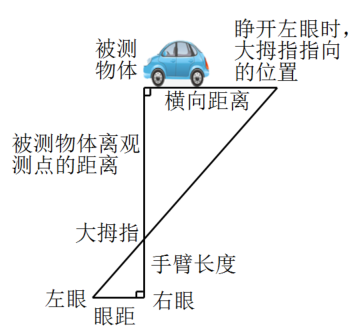
步骤:
第一步:水平举起右臂,大拇指紧直向上,大臂与身体垂直;
第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;
第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离的长度;
第四步:将横向距离乘以10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测,点的距离值.
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图,该汽车的长度大约为4米,则汽车到观测点的距离约为( )

中国营养学会推荐的三大营养素供能比参考值 | |
蛋白质 | 10%~15% |
脂肪 | 20%~30% |
碳水化合物 | 50%~65% |
注:供能比为某物质提供的能量占人体所需总能量的百分比.
梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中,
, 四边形
、
和
分别是以
的三边为一边的正方形.延长
和
, 交于点
, 连接
并延长交
于点
, 交
于点
, 延长
交
于点
.
如图2,四边形和
分别是以
的两边为一边的平行四边形,探索在
下方是否存在平行四边形
, 使得该平行四边形的面积等于平行四边形
、
的面积之和.若存在,作出满足条件的平行四边形
(保留适当的作图痕迹);若不存在,请说明理由.
小明在练习簿的横线上取点为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出了同心圆与横线的一些交点,如图1所示,他发现这些点的位置有一定的规律.
【提出问题】
小明通过观察,提出猜想:按此步骤继续画圆描点,所描的点都在某二次函数图象上.



小明利用已学知识和经验,以圆心为原点,过点
的横线所在直线为
轴,过点
且垂直于横线的直线为
轴,相邻横线的间距为一个单位长度,建立平面直角坐标系,如图2所示.当所描的点在半径为5的同心圆上时,其坐标为.
请帮助小明验证他的猜想是否成立.
小明继续思考:设点 ,
为正整数,以
为直径画
, 是否存在所描的点在
上.若存在,求
的值;若不存在,说明理由.
试题篮