2020年浙江省中考数学分类汇编专题06 二次函数

修改时间：2020-07-06 浏览次数：572 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 二次函数y=x²的图象平移后经过点（2，0），则下列平移方法正确的是（）

A . 向左平移2个单位，向下平移2个单位 B . 向左平移1个单位，向上平移2个单位 C . 向右平移1个单位，向下平移1个单位 D . 向右平移2个单位，向上平移1个单位

查看解析收藏纠错

+选题
2. 已知(-3，y₁)，(-2，y₂)，(1，y₃)是抛物线y=-3x²-12x+m上的点，则（）

A . y₃<y₂<y₁ B . y₃<y₁<y₂ C . y₂<y₃<y₁ D . y₁<y₃<y₂

查看解析收藏纠错

+选题
3. 在平面直角坐标系中，已知函数y₁=x²+ax+1，y₂=x²+bx+2，y₃=x²+cx+4，其中a，b，c是正实数，且满足b²=ac。设函数y₁ ， y₂ ， y₃的图象与x轴的交点个数分别为M₁ ， M₂ ， M₃ ，（）

A . 若M₁=2，M₂=2，则M₃=0 B . 若M₁=1，M₂=0，则M₃=0 C . 若M₁=0，M₂=2，则M₃=0 D . 若M₁=0，M₂=0，则M₃=0

查看解析收藏纠错

+选题
4. 设函数y=a(x-h)²+k(a，h，k是实数，a≠0)，当x=1时，y=1，当x=8时，y=8，（）

A . 若h=4，则a<0 B . 若h=5，则a>0 C . 若h=6，则a<0 D . 若h=7，则a>0

查看解析收藏纠错

+选题
5. 如图，二次函数 $\text{[math]}$ (a>0)的图象与x轴交于A，B两点，与y轴正半轴交于点C，它的对称轴为直线x=-1.则下列选项中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 当 $\text{[math]}$ (n为实数)时， $\text{[math]}$

查看解析收藏纠错

+选题

二、综合题

6. 如图1，在平面直角坐标系中，△ABC的顶点A，C分别是直线y= $\text{[math]}$ x+4与坐标轴的交点，点B的坐标为（-2，0）。点D是边AC上的一点，DE⊥BC于点E，点F在边AB上，且D，F两点关于y轴上的某点成中心对称，连结DF，EF。设点D的横坐标为m，EF²为l，请探究：

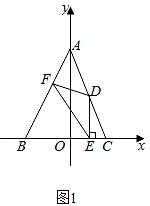
①线段EF长度是否有最小值。

②△BEF能否成为直角三角形。

小明尝试用“观察--猜想--验证--应用”的方法进行探究，请你一起来解决问题。

（1）小明利用“几何画板”软件进行观察，测量，得到l随m变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图2），请你在图2中连线，观察图象特征并猜想l与m可能满足的函数类别。

（2）小明结合图1，发现应用二角形和函数知识能验证（1）中的猜想.请你求出l关于m的函数表达式及自变量的取值范围，并求出线段EF长度的最小值。

（3）小明通过观察，推理，发现△BEF能成为直角三角形。请你求出当△BEF为直角三角形时m的值。

查看解析收藏纠错

+选题
7. 用各种盛水容器可以制作精致的家用流水景观（如图1）.科学原理：如图2，始终盛满水的圆体水桶水面离地面的高度为H（单位：cm），如果在离水面竖直距离为h（单位：cm）的地方开大小合适的小孔，那么从小孔射出水的射程（水流落地点离小孔的水平距离）s（单位：cm）与h的关系为s²=4h（H—h）.

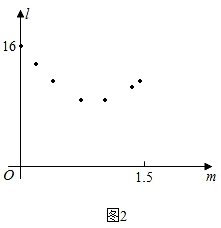
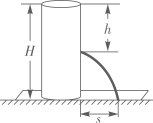
应用思考：现用高度为20cm的圆柱体望料水瓶做相关研究，水瓶直立地面，通过连注水保证它始终盛满水，在离水面竖直距高h cm处开一个小孔.

（1）写出s²与h的关系式；并求出当h为何值时，射程s有最大值，最大射程是多少?

（2）在侧面开两个小孔，这两个小孔离水面的竖直距离分别为a，b，要使两孔射出水的射程相同，求a，b之间的关系式；

（3）如果想通过垫高塑料水瓶，使射出水的最大射程增加16cm，求垫高的高度及小孔离水面的竖直距离.

查看解析收藏纠错

+选题
8. 已知抛物线y=ax²+bx+1经过点(1，-2)，(-2，13)。

（1）求a，b的值。

（2）若(5，y₁)，(m，y₂)是抛物线上不同的两点，且y₂=12-y₁ ，求m的值。

查看解析收藏纠错

+选题
9. 如图1，排球场长为18m，宽为9m，网高为2.24m，队员站在底线O点处发球，球从点O的正上方1.9m的C点发出，运动路线是抛物线的一部分，当球运动到最高点A时，高度为2.88m，即BA=2.88m，这时水平距离OB=7m，以直线OB为x轴，直线OC为y轴，建立平面直角坐标系，如图2。

（1）若球向正前方运动（即x轴垂直于底线)，求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围)，并判断这次发球能否过网？是否出界？说明理由。

（2）若球过网后的落点是对方场地①号位内的点P(如图1，点P距底线1m、边线0.5m)，问发球点O在底线上的哪个位置？(参考数据： $\text{[math]}$ 取1.4)

查看解析收藏纠错

+选题
10. 在平面直角坐标系中，设二次函数y₁=x²+bx+a，y₂=ax²+bx+1(a，b是实数，a≠0)。

（1）若函数y₁的对称轴为直线x=3，且函数y₁的图象经过点(a，b)，求函数y₁的表达式。

（2）若函数y₁的图象经过点(r，0)，其中r≠0，求证：函数y₂的图象经过点( $\text{[math]}$ ，0)。

（3）若函数y₁和函数y₂的最小值分别为m和n，若m+n=0，求m，n的值。

查看解析收藏纠错

+选题
11. 如图，在平面直角坐标系中，二次函数 $\text{[math]}$ 图象的顶点是A，与x轴交于B，C两点，与y轴交于点D.点B的坐标是(1，0).

（1）求A，C两点的坐标，并根据图象直接写出当y>0时x的取值范围.

（2）平移该二次函数的图象，使点D恰好落在点A的位置上，求平移后图象所对应的二次函数的表达式.

查看解析收藏纠错

+选题
12. 如图，已知在平面直角坐标系xOy中，抛物线 $\text{[math]}$ (c＞0)的顶点为D，与y轴的交点为C，过点C的直线CA与抛物线交于另一点A（点A在对称轴左侧），点B在AC的延长线上，连结OA，OB，DA和DB.

（1）如图1，当AC∥x轴时.①已知点A的坐标是(﹣2，1)，求抛物线的解析式；②若四边形AOBD是平行四边形，求证：b²＝4c.

（2）如图2，若b＝﹣2， $\text{[math]}$ ，是否存在这样的点A，使四边形AOBD是平行四边形？若存在，求出点A的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题
13. 如图，在平面直角坐标系中，已知二次函数图象的顶点为A，与y轴交于点B，异于顶点A的点C(1，n)在该函数图象上.

（1）当m=5时，求n的值.

（2）当n=2时，若点A在第一象限内，结合图象，求当y 时，自变量x的取值范围.

（3）作直线AC与y轴相交于点D.当点B在x轴上方，且在线段OD上时，求m的取值范围.

查看解析收藏纠错

+选题
14. 在篮球比赛中，东东投出的球在点A处反弹，反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系)，抛物线顶点为点B。

（1）求该抛物线的函数表达式。

（2）当球运动到点C时被东东抢到，CD⊥x轴于点D，CD=2.6m。
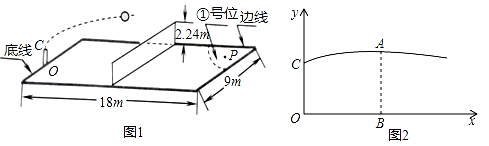
①求OD的长。

②东东抢到球后，因遭对方防守无法投篮，他在点D处垂直起跳传球，想将球沿直线快速传给队友华华，目标为华华的接球点E(4，1.3)。东东起跳后所持球离地面高度h₁(m)(传球前)与东东起跳后时间t(s)满足函数关系式h₁=-2(t-0.5)²+2.7(0≤t≤1)；小戴在点F(1.5，0)处拦截，他比东东晚0.3s垂直起跳，其拦截高度h₂(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同)。东东的直线传球能否越过小戴的拦截传到点E？若能，东东应在起跳后什么时间范围内传球？若不能，请说明理由(直线传球过程中球运动时间忽略不计)。

查看解析收藏纠错

+选题

2020年浙江省中考数学分类汇编专题06 二次函数

一、单选题

二、综合题

相关试卷 收起∨

相关试卷收起∨