2017年湖北省随州市中考数学试卷

1. ﹣2的绝对值是（）

A . 2 B . ﹣2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . a³+a³=a⁶ B . （a﹣b）²=a²﹣b² C . （﹣a³）²=a⁶ D . a¹²÷a²=a⁶

查看解析收藏纠错

+选题
3. 如图是某几何体的三视图，这个几何体是（）

A . 圆锥 B . 长方体 C . 圆柱 D . 三棱柱

查看解析收藏纠错

+选题
4. 一组数据2，3，5，4，4的中位数和平均数分别是（）

A . 4和3.5 B . 4和3.6 C . 5和3.5 D . 5和3.6

查看解析收藏纠错

+选题
5. 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（）

A . 两点之间线段最短 B . 两点确定一条直线 C . 垂线段最短 D . 经过直线外一点，有且只有一条直线与这条直线平行

查看解析收藏纠错

+选题
6. 如图，用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（）

A . 以点F为圆心，OE长为半径画弧 B . 以点F为圆心，EF长为半径画弧 C . 以点E为圆心，OE长为半径画弧 D . 以点E为圆心，EF长为半径画弧

查看解析收藏纠错

+选题
7. 小明到商店购买“五四青年节”活动奖品，购买20只铅笔和10本笔记本共需110元，但购买30支铅笔和5本笔记本只需85元，设每支铅笔x元，每本笔记本y元，则可列方程组（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 在公园内，牡丹按正方形种植，在它的周围种植芍药，如图反映了牡丹的列数（n）和芍药的数量规律，那么当n=11时，芍药的数量为（）

A . 84株 B . 88株 C . 92株 D . 121株

查看解析收藏纠错

+选题
9. 对于二次函数y=x²﹣2mx﹣3，下列结论错误的是（）

A . 它的图象与x轴有两个交点 B . 方程x²﹣2mx=3的两根之积为﹣3 C . 它的图象的对称轴在y轴的右侧 D . x＜m时，y随x的增大而减小

查看解析收藏纠错

+选题
10. 如图，在矩形ABCD中，AB＜BC，E为CD边的中点，将△ADE绕点E顺时针旋转180°，点D的对应点为C，点A的对应点为F，过点E作ME⊥AF交BC于点M，连接AM、BD交于点N，现有下列结论：
①AM=AD+MC；②AM=DE+BM；③DE²=AD•CM；④点N为△ABM的外心．其中正确的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题

11. 根据中央“精准扶贫”规划，每年要减贫约11700000人，将数据11700000用科学记数法表示为．

查看解析收藏纠错

+选题
12. “抛掷一枚质地均匀的硬币，正面向上”是事件（从“必然”、“随机”、“不可能”中选一个）．

查看解析收藏纠错

+选题
13. 如图，已知AB是⊙O的弦，半径OC垂直AB，点D是⊙O上一点，且点D与点C位于弦AB两侧，连接AD、CD、OB，若∠BOC=70°，则∠ADC=度．

查看解析收藏纠错

+选题
14. 在△ABC在，AB=6，AC=5，点D在边AB上，且AD=2，点E在边AC上，当AE=时，以A、D、E为顶点的三角形与△ABC相似．

查看解析收藏纠错

+选题
15.
如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（3，0）是OB上的一定点，点M是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为．

查看解析收藏纠错

+选题
16. 在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发2 $\text{[math]}$ h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是（填写所有正确结论的序号）．

查看解析收藏纠错

+选题

17. 计算：（ $\text{[math]}$ ）^﹣2﹣（2017﹣π）⁰+ $\text{[math]}$ ﹣|﹣2|．

查看解析收藏纠错

+选题
18. 解分式方程： $\text{[math]}$ +1= $\text{[math]}$ ．

查看解析收藏纠错

+选题
19.
如图，在平面直角坐标系中，将坐标原点O沿x轴向左平移2个单位长度得到点A，过点A作y轴的平行线交反比例函数y= $\text{[math]}$ 的图象于点B，AB= $\text{[math]}$ ．

（1）求反比例函数的解析式；

（2）若P（x₁ ， y₁）、Q（x₂ ， y₂）是该反比例函数图象上的两点，且x₁＜x₂时，y₁＞y₂ ，指出点P、Q各位于哪个象限？并简要说明理由．

查看解析收藏纠错

+选题
20.
风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A处测得塔杆顶端C的仰角是55°，沿HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的顶端D（D、C、H在同一直线上）的仰角是45°．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG为10米，BG⊥HG，CH⊥AH，求塔杆CH的高．（参考数据：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）

查看解析收藏纠错

+选题
21. 某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛，初赛后对选手成绩进行了整理，分成5个小组（x表示成绩，单位：分），A组：75≤x＜80；B组：80≤x＜85；C组：85≤x＜90；D组：90≤x＜95；E组：95≤x＜100．并绘制出如图两幅不完整的统计图．
请根据图中信息，解答下列问题：

（1）参加初赛的选手共有名，请补全频数分布直方图；

（2）扇形统计图中，C组对应的圆心角是多少度？E组人数占参赛选手的百分比是多少？

（3）学校准备组成8人的代表队参加市级决赛，E组6名选手直接进入代表队，现要从D组中的两名男生和两名女生中，随机选取两名选手进入代表队，请用列表或画树状图的方法，求恰好选中一名男生和一名女生的概率．

查看解析收藏纠错

+选题
22. 如图，在Rt△ABC中，∠C=90°，AC=BC，点O在AB上，经过点A的⊙O与BC相切于点D，交AB于点E．

（1）求证：AD平分∠BAC；

（2）若CD=1，求图中阴影部分的面积（结果保留π）．

查看解析收藏纠错

+选题

23. 某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．

（1）求该种水果每次降价的百分率；

（2）从第一次降价的第1天算起，第x天（x为整数）的售价、销量及储存和损耗费用的相关信息如表所示．已知该种水果的进价为4.1元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1≤x＜15）之间的函数关系式，并求出第几天时销售利润最大？

时间x（天）	1≤x＜9	9≤x＜15	x≥15
售价（元/斤）	第1次降价后的价格	第2次降价后的价格
销量（斤）	80﹣3x	120﹣x
储存和损耗费用（元）	40+3x	3x²﹣64x+400

（3）在（2）的条件下，若要使第15天的利润比（2）中最大利润最多少127.5元，则第15天在第14天的价格基础上最多可降多少元？

查看解析收藏纠错

+选题

24.
如图，分别是可活动的菱形和平行四边形学具，已知平行四边形较短的边与菱形的边长相等．

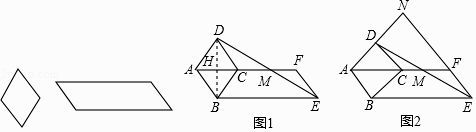
（1）在一次数学活动中，某小组学生将菱形的一边与平行四边形较短边重合，摆拼成如图1所示的图形，AF经过点C，连接DE交AF于点M，观察发现：点M是DE的中点．
下面是两位学生有代表性的证明思路：
思路1：不需作辅助线，直接证三角形全等；
思路2：不证三角形全等，连接BD交AF于点H．…
请参考上面的思路，证明点M是DE的中点（只需用一种方法证明）；

（2）如图2，在（1）的前提下，当∠ABE=135°时，延长AD、EF交于点N，求 $\text{[math]}$ 的值；

（3）在（2）的条件下，若 $\text{[math]}$ =k（k为大于 $\text{[math]}$ 的常数），直接用含k的代数式表示 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
25.
在平面直角坐标系中，我们定义直线y=ax﹣a为抛物线y=ax²+bx+c（a、b、c为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．
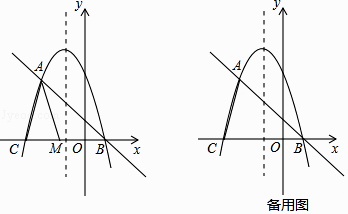
已知抛物线y=﹣ $\text{[math]}$ x²﹣ $\text{[math]}$ x+2 $\text{[math]}$ 与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C．

（1）填空：该抛物线的“梦想直线”的解析式为，点A的坐标为，点B的坐标为；

（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；

（3）当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

2017年湖北省随州市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

2017年湖北省随州市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨