福建省2018年中考数学试卷（A卷）

1. 在实数|﹣3|，﹣2，0，π中，最小的数是（）

A . |﹣3| B . ﹣2 C . 0 D . π

查看解析收藏纠错

+选题
2. 某几何体的三视图如图所示，则该几何体是（）

A . 圆柱 B . 三棱柱 C . 长方体 D . 四棱锥

查看解析收藏纠错

+选题
3. 下列各组数中，能作为一个三角形三边边长的是（）

A . 1，1，2 B . 1，2，4 C . 2，3，4 D . 2，3，5

查看解析收藏纠错

+选题
4. 一个n边形的内角和为360°，则n等于（）

A . 3 B . 4 C . 5 D . 6

查看解析收藏纠错

+选题
5. 如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（）

A . 15° B . 30° C . 45° D . 60°

查看解析收藏纠错

+选题
6. 投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）

A . 两枚骰子向上一面的点数之和大于1 B . 两枚骰子向上一面的点数之和等于1 C . 两枚骰子向上一面的点数之和大于12 D . 两枚骰子向上一面的点数之和等于12

查看解析收藏纠错

+选题
7. 已知m= $\text{[math]}$ + $\text{[math]}$ ，则以下对m的估算正确的（）

A . 2＜m＜3 B . 3＜m＜4 C . 4＜m＜5 D . 5＜m＜6

查看解析收藏纠错

+选题
8. 我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，则符合题意的方程组是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，AB是⊙O的直径，BC与⊙O相切于点B，AC交⊙O于点D，若∠ACB=50°，则∠BOD等于（）

A . 40° B . 50° C . 60° D . 80°

查看解析收藏纠错

+选题
10. 已知关于x的一元二次方程（a+1）x²+2bx+（a+1）=0有两个相等的实数根，下列判断正确的是（）

A . 1一定不是关于x的方程x²+bx+a=0的根 B . 0一定不是关于x的方程x²+bx+a=0的根 C . 1和﹣1都是关于x的方程x²+bx+a=0的根 D . 1和﹣1不都是关于x的方程x²+bx+a=0的根

查看解析收藏纠错

+选题

11. 计算：（ $\text{[math]}$ ）⁰﹣1=．

查看解析收藏纠错

+选题
12. 某8种食品所含的热量值分别为：120，134，120，119，126，120，118，124，则这组数据的众数为．

查看解析收藏纠错

+选题
13. 如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD=．

查看解析收藏纠错

+选题
14. 不等式组 $\text{[math]}$ 的解集为．

查看解析收藏纠错

+选题
15. 把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB= $\text{[math]}$ ，则CD=．

查看解析收藏纠错

+选题
16. 如图，直线y=x+m与双曲线y= $\text{[math]}$ 相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为．

查看解析收藏纠错

+选题

17. 解方程组： $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 如图，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F．求证：OE=OF．

查看解析收藏纠错

+选题
19. 先化简，再求值：（ $\text{[math]}$ ﹣1）÷ $\text{[math]}$ ，其中m= $\text{[math]}$ +1．

查看解析收藏纠错

+选题
20. 求证：相似三角形对应边上的中线之比等于相似比．
要求：
①根据给出的△ABC及线段A'B′，∠A′（∠A′=∠A），以线段A′B′为一边，在给出的图形上用尺规作出△A'B′C′，使得△A'B′C′∽△ABC，不写作法，保留作图痕迹；
②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程．

查看解析收藏纠错

+选题
21. 如图，在Rt△ABC中，∠C=90°，AB=10，AC=8．线段AD由线段AB绕点A按逆时针方向旋转90°得到，△EFG由△ABC沿CB方向平移得到，且直线EF过点D．

（1）求∠BDF的大小；

（2）求CG的长．

查看解析收藏纠错

+选题
22. 甲、乙两家快递公司揽件员（揽收快件的员工）的日工资方案如下：
甲公司为“基本工资+揽件提成”，其中基本工资为70元/日，每揽收一件提成2元；
乙公司无基本工资，仅以揽件提成计算工资．若当日揽件数不超过40，每件提成4元；若当日搅件数超过40，超过部分每件多提成2元．如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图：

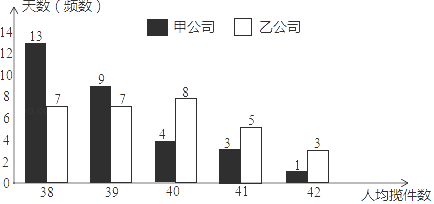
（1）现从今年四月份的30天中随机抽取1天，求这一天甲公司揽件员人均揽件数超过40（不含40）的概率；

（2）根据以上信息，以今年四月份的数据为依据，并将各公司揽件员的人均揽件数视为该公司各揽件员的揽件数，解决以下问题：
①估计甲公司各揽件员的日平均件数；
②小明拟到甲、乙两家公司中的一家应聘揽件员，如果仅从工资收入的角度考虑，请利用所学的统计知识帮他选择，井说明理由．

查看解析收藏纠错

+选题
23. 如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

（1）若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；

（2）求矩形菜园ABCD面积的最大值．

查看解析收藏纠错

+选题
24. 已知四边形ABCD是⊙O的内接四边形，AC是⊙O的直径，DE⊥AB，垂足为E．

（1）延长DE交⊙O于点F，延长DC，FB交于点P，如图1．求证：PC=PB；

（2）过点B作BC⊥AD，垂足为G，BG交DE于点H，且点O和点A都在DE的左侧，如图2．若AB= $\text{[math]}$ ，DH=1，∠OHD=80°，求∠BDE的大小．

查看解析收藏纠错

+选题
25. 已知抛物线y=ax²+bx+c过点A（0，2）．

（1）若点（﹣ $\text{[math]}$ ，0）也在该抛物线上，求a，b满足的关系式；

（2）若该抛物线上任意不同两点M（x₁ ， y₁），N（x₂ ， y₂）都满足：当x₁＜x₂＜0时，（x₁﹣x₂）（y₁﹣y₂）＞0；当0＜x₁＜x₂时，（x₁﹣x₂）（y₁﹣y₂）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．
①求抛物线的解析式；
②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．

查看解析收藏纠错

+选题

福建省2018年中考数学试卷（A卷）

一、选择题

二、细心填一填

三、专心解一解

相关试卷收起∨

福建省2018年中考数学试卷（A卷）

一、选择题

二、细心填一填

三、专心解一解

相关试卷 收起∨

相关试卷收起∨