四川省达州市2018年中考数学试卷

1. 2018的相反数是（）

A . 2018 B . ﹣2018 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 二次根式 $\text{[math]}$ 中的x的取值范围是（）

A . x＜﹣2 B . x≤﹣2 C . x＞﹣2 D . x≥﹣2

查看解析收藏纠错

+选题
3. 下列图形中是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 如图，AB∥CD，∠1=45°，∠3=80°，则∠2的度数为（）

A . 30° B . 35° C . 40° D . 45°

查看解析收藏纠错

+选题
5. 下列说法正确的是（）

A . “打开电视机，正在播放《达州新闻》”是必然事件 B . 天气预报“明天降水概率50%，是指明天有一半的时间会下雨” C . 甲、乙两人在相同的条件下各射击10次，他们成绩的平均数相同，方差分别是S²=0.3，S²=0.4，则甲的成绩更稳定 D . 数据6，6，7，7，8的中位数与众数均为7

查看解析收藏纠错

+选题
6. 平面直角坐标系中，点P的坐标为（m，n），则向量 $\text{[math]}$ 可以用点P的坐标表示为 $\text{[math]}$ =（m，n）；已知 $\text{[math]}$ =（x₁ ， y₁）， $\text{[math]}$ =（x₂ ， y₂），若x₁x₂+y₁y₂=0，则 $\text{[math]}$ 与 $\text{[math]}$ 互相垂直．下面四组向量：① $\text{[math]}$ =（3，﹣9）， $\text{[math]}$ =（1，﹣ $\text{[math]}$ ）；② $\text{[math]}$ =（2，π⁰）， $\text{[math]}$ =（2^﹣¹ ， ﹣1）；③ $\text{[math]}$ =（cos30°，tan45°）， $\text{[math]}$ =（sin30°，tan45°）；④ $\text{[math]}$ =（ $\text{[math]}$ +2， $\text{[math]}$ ）， $\text{[math]}$ =（ $\text{[math]}$ ﹣2， $\text{[math]}$ ）．其中互相垂直的组有（）

A . 1组 B . 2组 C . 3组 D . 4组

查看解析收藏纠错

+选题
7. 如图，在物理课上，老师将挂在弹簧测力计下端的铁块浸没于水中，然后缓慢匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧测力计的读数y（单位：N）与铁块被提起的高度x（单位：cm）之间的函数关系的大致图象是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 3

查看解析收藏纠错

+选题
9. 如图，E，F是平行四边形ABCD对角线AC上两点，AE=CF= $\text{[math]}$ AC．连接DE，DF并延长，分别交AB，BC于点G，H，连接GH，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

查看解析收藏纠错

+选题
10. 如图，二次函数y=ax²+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：abc＜0；②9a+3b+c＞0；③若点M（ $\text{[math]}$ ，y₁），点N（ $\text{[math]}$ ，y₂）是函数图象上的两点，则y₁＜y₂；④﹣ $\text{[math]}$ ＜a＜﹣ $\text{[math]}$ ．其中正确结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题

11. 受益于电子商务发展和法治环境改善等多重因素，快递业务迅猛发展．预计达州市2018年快递业务量将达到5.5亿件，数据5.5亿用科学记数法表示为．

查看解析收藏纠错

+选题
12. 已知a^m=3，aⁿ=2，则a^2m^﹣ⁿ的值为．

查看解析收藏纠错

+选题
13. 若关于x的分式方程 $\text{[math]}$ =2a无解，则a的值为．

查看解析收藏纠错

+选题
14. 如图，平面直角坐标系中，矩形OABC的顶点A（﹣6，0），C（0，2 $\text{[math]}$ ）．将矩形OABC绕点O顺时针方向旋转，使点A恰好落在OB上的点A₁处，则点B的对应点B₁的坐标为．

查看解析收藏纠错

+选题
15. 已知：m²﹣2m﹣1=0，n²+2n﹣1=0且mn≠1，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
16. 如图，Rt△ABC中，∠C=90°，AC=2，BC=5，点D是BC边上一点且CD=1，点P是线段DB上一动点，连接AP，以AP为斜边在AP的下方作等腰Rt△AOP．当P从点D出发运动至点B停止时，点O的运动路径长为．

查看解析收藏纠错

+选题

17. 计算：（﹣1）²⁰¹⁸+（﹣ $\text{[math]}$ ）^﹣²﹣|2﹣ $\text{[math]}$ |+4sin60°；

查看解析收藏纠错

+选题
18. 化简代数式： $\text{[math]}$ ，再从不等式组 $\text{[math]}$ 的解集中取一个合适的整数值代入，求出代数式的值．

查看解析收藏纠错

+选题
19. 为调查达州市民上班时最常用的交通工具的情况，随机抽取了部分市民进行调查，要求被调查者从“A：自行车，B：电动车，C：公交车，D：家庭汽车，E：其他”五个选项中选择最常用的一项．将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题．

（1）本次调查中，一共调查了名市民；扇形统计图中，B项对应的扇形圆心角是度；补全条形统计图；

（2）若甲、乙两人上班时从A，B，C，D四种交通工具中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两人恰好选择同一种交通工具上班的概率．

查看解析收藏纠错

+选题
20. 在数学实践活动课上，老师带领同学们到附近的湿地公园测量园内雕塑的高度．用测角仪在A处测得雕塑顶端点C′的仰角为30°，再往雕塑方向前进4米至B处，测得仰角为45°．问：该雕塑有多高？（测角仪高度忽略不计，结果不取近似值．）

查看解析收藏纠错

+选题
21. “绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的50%标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．

（1）求该型号自行车的进价和标价分别是多少元？

（2）若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？

查看解析收藏纠错

+选题
22. 已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F．

（1）求证：DF是⊙O的切线；

（2）若等边△ABC的边长为8，求由弧DE、DF、EF围成的阴影部分面积．

查看解析收藏纠错

+选题
23. 矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y= $\text{[math]}$ （k＞0）的图象与边AC交于点E．

（1）当点F运动到边BC的中点时，求点E的坐标；

（2）连接EF，求∠EFC的正切值；

（3）如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式．

查看解析收藏纠错

+选题
24. 阅读下列材料：
已知：如图1，等边△A₁A₂A₃内接于⊙O，点P是弧A₁A ₂ 上的任意一点，连接PA₁ ， PA₂ ， PA₃ ，可证：PA₁+PA₂=PA₃ ，从而得到： $\text{[math]}$ 是定值．

（1）以下是小红的一种证明方法，请在方框内将证明过程补充完整；
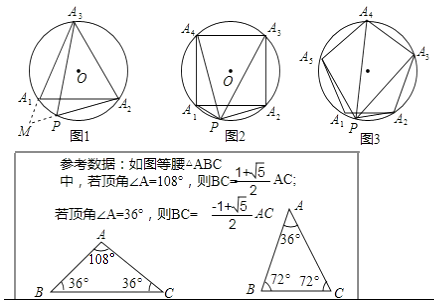
证明：如图1，作∠PA₁M=60°，A₁M交A₂P的延长线于点M．
∵△A₁A₂A₃是等边三角形，
∴∠A₃A₁A₂=60°，
∴∠A₃A₁P=∠A₂A₁M
又A₃A₁=A₂A₁ ， ∠A₁A₃P=∠A₁A₂P，
∴△A₁A₃P≌△A₁A₂M
∴PA₃=MA₂=PA₂+PM=PA₂+PA₁ ．
∴ $\text{[math]}$ ，是定值．

（2）延伸：如图2，把（1）中条件“等边△A₁A₂A₃”改为“正方形A₁A₂A₃A₄”，其余条件不变，请问： $\text{[math]}$ 还是定值吗？为什么？

（3）拓展：如图3，把（1）中条件“等边△A₁A₂A₃”改为“正五边形A₁A₂A₃A₄A₅”，其余条件不变，则 $\text{[math]}$ =（只写出结果）．

查看解析收藏纠错

+选题
25. 如图，抛物线经过原点O（0，0），点A（1，1），点B（ $\text{[math]}$ ，0）．

（1）求抛物线解析式；

（2）连接OA，过点A作AC⊥OA交抛物线于C，连接OC，求△AOC的面积；

（3）点M是y轴右侧抛物线上一动点，连接OM，过点M作MN⊥OM交x轴于点N．问：是否存在点M，使以点O，M，N为顶点的三角形与（2）中的△AOC相似，若存在，求出点M的坐标；若不存在，说明理由．

查看解析收藏纠错

+选题

四川省达州市2018年中考数学试卷

一、单项选择题

二、填空题

三、解答题

相关试卷收起∨

四川省达州市2018年中考数学试卷

一、单项选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨