注册

题型：填空题题类：难易度：困难

湖北省武汉市江岸区2022-2023学年八年级下学期期末数学试题

如图所示，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， E为 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 $\text{[math]}$ ．

举一反三

如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC于点D，CD=3，则BC的长为（）

若等腰三角形的两条边的长分别为5cm和8cm，则它的周长是（）

已知：如图，四边形ABCD中，点C在AB的延长线上，连接DC．∠EDC=∠C，AD∥BE．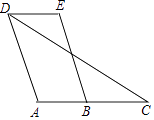

求证：∠A=∠E．

证明：∵∠EDC=∠C，

∴AB∥{#blank#}1{#/blank#}．（{#blank#}2{#/blank#}）

∴{#blank#}3{#/blank#} ={#blank#}4{#/blank#}．（{#blank#}5{#/blank#}）

∵AD∥BE，

∴∠A={#blank#}6{#/blank#}．（{#blank#}7{#/blank#}）

∴∠A=∠E．（等量代换）

如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积是24， $\text{[math]}$ 的垂直平分线 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 边于点 $\text{[math]}$ ， $\text{[math]}$ ，若点 $\text{[math]}$ 为 $\text{[math]}$ 边的中点，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

如图， $\text{[math]}$ 中，OD、OE分别是AB、BC边上的垂直平分线，OD、OE交于点O，连接OA、OC，已知 $\text{[math]}$ ，则 $\text{[math]}$ {#blank#}1{#/blank#}．

如图，在 $\text{[math]}$ 中， $\text{[math]}$ 边的垂直平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 边的垂直半分线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 的周长为 $\text{[math]}$ ， $\text{[math]}$ 的周长为 $\text{[math]}$ ．

返回首页

相关试卷

试题篮

公司介绍

Company Introduction

服务介绍

Service Introduction

帮助中心

Help center

二一教育APP

二一教育APP

400-637-9991

周一至周五 8:30-17:30

在线咨询客服