浙教版数学八升九暑假每天一测预习篇：二次函数的应用

1. 如表给出了二次函数y＝ax²+bx+c（a≠0）中x ， y的一些对应值，则可以估计一元二次方程ax²+bx+c＝0（a≠0）的一个近似解x₁的范围为（）
x
…
1.2
1.3
1.4
1.5
1.6
…
y
…
﹣1.16
﹣0.71
﹣0.24
0.25
0.76
…

A . 1.2＜x₁＜1.3 B . 1.3＜x₁＜1.4 C . 1.4＜x₁＜1.5 D . 1.5＜x₁＜1.6

查看解析收藏纠错

+选题
2. 抛物线y＝x²＋ax＋3的对称轴为直线x＝1.若关于x的方程x²＋ax＋3﹣t＝0（t为实数），在﹣2＜x＜3的范围内有实数根，则t的取值范围是（）

A . 6＜t＜11 B . t≥2 C . 2≤t＜11 D . 2≤t＜6

查看解析收藏纠错

+选题
3. 已知m=6，关于x的一元二次方程(x+3)(x－4)－m＝0的解为x₁ ， x₂（x₁＜x₂），则下列结论正确的是（）

A . x₁＜－3＜4＜x₂ B . －3＜x₁＜4＜x₂ C . －3＜x₁＜x₂＜4 D . x₁＜－3＜x₂＜4

查看解析收藏纠错

+选题
4. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，记 $\text{[math]}$ ，则其面积 $\text{[math]}$ ，这个公式也被称为海伦一秦九韶公式 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则此三角形面积的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 某网店销售一款李宁牌运动服，每件进价 $\text{[math]}$ 元，若按每件 $\text{[math]}$ 元出售，每天可卖出 $\text{[math]}$ 件，根据市场调查结果，若每件降价 $\text{[math]}$ 元，则每天可多卖出 $\text{[math]}$ 件，要使每天获得的利润最大，则每件需要降价的钱数为（）

A . 3元 B . 4元 C . 5元 D . 8元

查看解析收藏纠错

+选题
6. 我校门口道路的隔离栏通常会涂上醒目的颜色，呈抛物线形状，如图是一个长为2米，宽为1米的矩形隔离栏，中间被4根栏杆五等分，每根栏杆的下面一部分涂上醒目的蓝色，颜色的分界处（点E ，点P）以及点A ，点B落上同一条抛物线上，若第1根栏杆涂色部分（EF）与第2根栏杆未涂色部分（PQ）长度相等，则EF的长度是（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

查看解析收藏纠错

+选题
7. 某商店购进某种商品的价格是7.5元/件，在一段时间里，单价是13.5元，销售量是500件，而单价每降低1元就可多售出200件，当销售价为x元/件时，获利润y元，则y与x的函数关系为（）

A . y＝（6-x）（500+x） B . y＝（13.5-x）（500+200x） C . y＝（6-x）（500+200x） D . 以上答案都不对

查看解析收藏纠错

+选题
8. 如图是抛物线形拱桥的示意图，已知水面宽4m，顶点离水面2m．当水面宽6m时，水面下降（）

A . 1m B . 1.5m C . 2.5m D . 4.5m

查看解析收藏纠错

+选题
9. 如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t² ，方程20t﹣5t²＝15的两根为t₁＝1与t₂＝3，下列对正确的是（）

A . 小球的飞行高度为15m时，小球飞行的时间是1s B . 小球飞行3s时飞行高度为15m，并将继续上升 C . 小球从飞出到落地要用4s D . 小球的飞行高度可以达到25m

查看解析收藏纠错

+选题
10. 如图，公园中一正方形水池中有一喷泉，喷出的水流呈抛物线状，测得喷出口高出水面0.8m，水流在离喷出口的水平距离1.25m处达到最高，密集的水滴在水面上形成了一个半径为3m的圆，考虑到出水口过高影响美观，水滴落水形成的圆半径过大容易造成水滴外溅到池外，现决定通过降低出水口的高度，使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面（）

A . 0.55米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . 0.4米

查看解析收藏纠错

+选题

11. 如图，二次函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ 两点，则关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的解为．

查看解析收藏纠错

+选题
12. 二次函数 $\text{[math]}$ 的部分对应值列表如下：
x
……
$\text{[math]}$
0
1
3
5
……
y
……
7
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
7

则一元二次方程 $\text{[math]}$ 的解为．

查看解析收藏纠错

+选题
13. 以初速度 $\text{[math]}$ （单位： $\text{[math]}$ 从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度 $\text{[math]}$ （单位：m）与小球的运动时间 $\text{[math]}$ （单位：s）之间的关系式是 $\text{[math]}$ ．现将某弹性小球从地面竖直向上抛出，初速度为 $\text{[math]}$ ，经过时间 $\text{[math]}$ 落回地面，运动过程中小球的最大高度为 $\text{[math]}$ ；小球落地后，竖直向上弹起，初速度为 $\text{[math]}$ ，经过时间 $\text{[math]}$ 落回地面，运动过程中小球的最大高度为 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
14. 在综合实践活动中，同学们借助如图所示的直角墙角（两边足够长），用24m长的篱笆围成一个矩形花园ABCD，则矩形花园ABCD的最大面积为m².

查看解析收藏纠错

+选题
15. 图1是洞头深门大桥，其桥底呈抛物线，以O为原点，OA所在直线为x轴建立平面直角坐标系（如图2所示），桥面CB∥OA，其抛物线解析式为 $\text{[math]}$ ，抛物线上点A离桥面距离AB＝22米，若存在一点E使得 $\text{[math]}$ ，则点E到抛物线的距离ED＝米．

查看解析收藏纠错

+选题
16. 2023年5月8日，C919商业首航完成.12时31分航班抵达北京首都机场，穿过隆重的“水门礼”.如图①，在一次“水门礼”的预演中，两辆消防车面向飞机喷射水柱，喷射的两条水柱近似看作形状相同的地物线的一部分．如图②，当两辆消防车喷水口A、B的水平距离为80米时，两条水柱在抛物线的顶点 $\text{[math]}$ 处相遇，此时相遇点 $\text{[math]}$ 距地面20米，喷水口A、B距地面均为4米.若两辆消防车同时后退10米，两条水柱的形状及喷水口 $\text{[math]}$ 、 $\text{[math]}$ 到地面的距离均保持不变，此时两条水柱相遇点 $\text{[math]}$ 距地面米.

查看解析收藏纠错

+选题

17. 跳长绳时，当绳甩到最高处时的形状是抛物线，如图正在甩绳的两名同学拿绳的手间距AB $\text{[math]}$ 为8米，手到地面的距离AO $\text{[math]}$ 和BD $\text{[math]}$ 均为0.8 $\text{[math]}$ 米，身高为1.5 $\text{[math]}$ 米的小红站在距点O的水平距离为1米的点F处，绳子甩到最高处时刚好通过她的头顶点E ，以点O为原点建立如图所示的平面直角坐标系，设此抛物线的解析式为 $\text{[math]}$ $\text{[math]}$ .

（1）求该抛物线的解析式.

（2）当绳子甩到最高处时，计算绳子与地面的最大距离.

（3）如果小明站在OD $\text{[math]}$ 之间，且离点O的距离为3米，当绳子甩到最高处时刚好通过他的头顶正上方0.6 $\text{[math]}$ 米处，求小明的身高.

查看解析收藏纠错

+选题
18. 某农场拟建两间矩形种牛饲养室，饲养室的一面靠现有墙（墙长＞50m），中间用一道墙隔开（如图），已知计划中的建筑材料可建围墙的总长为50m，设两饲养室合计长x（m），总占地面积为y（m²）

（1）求y关于x的函数表达式和自变量的取值范围；

（2）若要使两间饲养室占地总面积达到200m² ，则x为多少？占地总面积有可能达到210m²吗？

查看解析收藏纠错

+选题
19. 某商店销售进价为40元/件的某种商品，在第 $\text{[math]}$ 天的售价与销量的相关信息如下表：
时间 $\text{[math]}$ （天）
$\text{[math]}$
$\text{[math]}$
售价（元/件）
$\text{[math]}$
80
每天销量（件）
$\text{[math]}$
设销售商品的每天利润为 $\text{[math]}$ 元．

（1）求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；

（2）问该商品第几天时，当天销售利润最大，最大利润是多少？

（3）现该商店决定每销售1件该商品就捐赠 $\text{[math]}$ 元 $\text{[math]}$ 给贫困地区，在销售的前30天内该商店当日最大利润为2312元，直接写出 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
20. 如图，已知排球场的长度OD为18米，位于球场中线处的球网AB的高度2.43米，一队员站在点O处发球，排球从点O的正上方1.8米的C点向正前方飞去，排球的飞行路线是抛物线的一部分，当排球运行至离点O的水平距离OE为7米时，到达最高点G，以O为原点建立如图所示的平面直角坐标系.

（1）若排球运行的最大高度为3.2米，求排球飞行的高度y(单位：米)与水平距离x(单位：米)之间的函数关系式(不要求写自变量x的取值范围)；

（2）在(1)的条件下，这次所发的球能够过网吗?如果能够过网，是否会出界?请说明理由；

（3）若队员发球既要过球网，排球又不会出界(排球压线属于没出界)，求二次函数中二次项系数的范围.

查看解析收藏纠错

+选题
21. 在卡塔尔世界杯期间，图1是某足球运动员在比赛期间的进球瞬间，足球在抽射过程中恰好碰到防守队员的身体，改变足球线路，弹射入网.小冲在训练过程中也尝试这样的射门，如图2是小冲在训练时的示意图，足球在空中的运动轨迹可以抽象成一条抛物线，假设足球在碰到障碍平台后的运动轨迹，与末碰到障碍平台前的轨迹的形状完全相同，且达到最高点时离地高度也相同，并且两条轨迹在同一平面内，射门时的起脚点 $\text{[math]}$ 与障碍平台 $\text{[math]}$ 之间的距离 $\text{[math]}$ 为 $\text{[math]}$ ，障碍平台高为 $\text{[math]}$ ，若小冲此次训练时足球正好在前方 $\text{[math]}$ 的点 $\text{[math]}$ 处达到最高点，离地面最高距离为 $\text{[math]}$ ，以地面 $\text{[math]}$ 所在直线为 $\text{[math]}$ 轴，过点 $\text{[math]}$ 且垂直于 $\text{[math]}$ 的直线为 $\text{[math]}$ 轴建立平面直角坐标系.

（1）求过O，C，B三点的抛物线表达式；

（2）此时障碍平台与球门之间的距离 $\text{[math]}$ 为 $\text{[math]}$ ，已知球门高为 $\text{[math]}$ ，请你通过计算，（不考虑其他因素）足球在经过障碍平台的反弹后能否顺利射入球门.

查看解析收藏纠错

+选题
22. 卡塔尔世界杯期间，主办方向中国某企业订购1万幅边长为4米的正方形作品 $\text{[math]}$ ，其设计图案如图所示（四周阴影是四个全等的矩形，用材料甲；中心区是正方形 $\text{[math]}$ ，用材料乙）.在厚度保持相同的情况下，两种材料的消耗成本如下表

材料

甲

乙

价格（元/米²）

60

30

设矩形的较短边 $\text{[math]}$ 的长为x米，制作一幅作品的材料费用为y元.

（1） $\text{[math]}$ 的长为米（用含x的代数式表示）；

（2）求y关于x的函数解析式，并写出自变量x的取值范围；

（3）当中心区的边长不小于3时，预备材料的购买资金700万够用吗？通过运算，请写出你的理由.

查看解析收藏纠错

+选题

23. 根据以下素材，探索完成任务．

素材1	某学校一块劳动实践基地大棚的横截面如图所示，上部分的顶棚是抛物线形状，下部分是由两根立柱 $\text{[math]}$ 和 $\text{[math]}$ 组成，立柱高为 $\text{[math]}$ ，顶棚最高点距离地面 $\text{[math]}$ 是 $\text{[math]}$ ， $\text{[math]}$ 的长为 $\text{[math]}$ ．
素材2	为提高灌溉效率，学校在 $\text{[math]}$ 的中点 $\text{[math]}$ 处安装了一款可垂直升降的自动喷灌器 $\text{[math]}$ ，从喷水口 $\text{[math]}$ 喷出的水流可以看成抛物线，其形状与 $\text{[math]}$ 的图象相同， $\text{[math]}$ ，此时水流刚好喷到立柱的端点 $\text{[math]}$ 处．
问题解决
任务1	确定顶棚的形状	以顶棚最高点为坐标原点建立平面直角坐标系，求出顶棚部分抛物线的表达式．
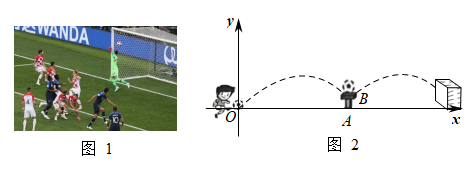
任务2	探索喷水的高度	问 $\text{[math]}$ 处喷出的水流在距离 $\text{[math]}$ 点水平距离为多少米时达到最高．
任务3	调整喷头的高度	如何调整喷水口的高度（形状不变），使水流喷灌时恰好落在边缘 $\text{[math]}$ 处．

查看解析收藏纠错

+选题

24. 根据以下素材，探索完成任务．

如何设计警戒线之间的宽度？
素材1	图1为某公园的抛物线型拱桥，图2是其横截面示意图，测得水面宽度AB=24米，拱顶离水面的距离为CD=4米．
素材2	拟在公园里投放游船供游客乘坐，载重最少时，游船的横截面如图3所示，漏出水面的船身为矩形，船顶为等腰三角形．测得相关数据如下：EF=EK=1.7米，FK=3米， GH=IJ=1.26米，FG=JK=0.4米．
素材3	为确保安全，拟在石拱桥下面的P ， Q两处设置航行警戒线，要求如下： ①游船底部HI在P ， Q之间通行； ②当载重最少通过时，游船顶部E与拱桥的竖直距离至少为0.5米．

问题解决

（1）任务1：确定拱桥形状

在图2中建立合适的直角坐标系，并求这条抛物线的函数表达式．

（2）任务2：设计警戒线之间的宽度

求PQ的最大值．

查看解析收藏纠错

+选题

浙教版数学八升九暑假每天一测预习篇：二次函数的应用

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共6题，共42分）

四、实践探究题（共2题，共24分）

相关试卷收起∨

x	……	$\text{[math]}$	0	1	3	5	……
y	……	7	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	7

时间 $\text{[math]}$ （天）	$\text{[math]}$	$\text{[math]}$
售价（元/件）	$\text{[math]}$	80
每天销量（件）	$\text{[math]}$

x	…	1.2	1.3	1.4	1.5	1.6	…
y	…	﹣1.16	﹣0.71	﹣0.24	0.25	0.76	…

材料	甲	乙
价格（元/米²）	60	30

浙教版数学八升九暑假每天一测预习篇：二次函数的应用

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共6题，共42分）

四、实践探究题（共2题，共24分）

相关试卷 收起∨

相关试卷收起∨