修改时间:2024-06-03 浏览次数:29 类型:复习试卷
问题情境:学习完平行四边形的性质和判定后,老师创设了如下探究情境,探究三角形的中位线定理.
问题1:如图1,在中,对角线AC,BD相交于点O,E为AB上一点,连接EO并延长交CD于F,则OE与OF有怎样的数量关系?

小明: .
理由如下:∵四边形ABCD是平行四边形,
∴ ,
(依据1)
∴
又∵ ,
∴(依据2).
∴
问题2:如图2,若点E为AB的中点,其他条件不变,则线段EF与BC有怎样的数量关系和位置关系?
小亮: ,
BC.
理由如下:….
问题3:如图3,在中,D,E分别是AB,AC的中点,连接DE,像DE这样,连接三角形两边中点的线段叫做三角形的中位线.通过前面问题给你的启发,你能猜想出DE和BC的数量关系和位置关系吗?
小慧:BC,
.
…
数学思考:
依据1:;依据2:.
请用图3写出三角形中位线定理的证明过程.
如图1, , 其中
,
, 此时,点
与点
重合.

①时,求证:
为等边三角形;
②当 时,
. (直接回答即可)

【问题情境】
在数学综合实践课上,老师让同学用两张全等的等腰三角形纸片进行拼摆,并探究摆放后所构成的图形之间的关系.如图1, ,
,
.
“勤奋小组”的同学把这两张纸片按如图2的方式摆放,点A与点D重合,连接 和
. 他们发现
和
之间存在着一定的数量关系,这个关系是.
“创新小组”的同学在“勤奋小组”的启发下,把这两张纸片按如图3的方式摆放,点F,A,D,C在同一直线上,连接 和
, 他们发现了
和
之间的数量和位置关系,请写出这些关系并说明理由;
请你利用 和
纸片进行拼摆,将拼摆出的图形画在图4中(要求不得与图2,图3相同),并根据图形写出一条正确的数学结论.
已知,等腰三角形纸片ABC中,AB=AC,∠BAC=36°.现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应任务.

作法:如图1所示, ①分别作AB,AC的垂直平分线,交于点P; ②连接PA,PB,PC. 结论:沿线段PA,PB,PC剪开,即可得到三个等腰三角形, 理由:∵点P在线段AB的垂直平分线上, ∴…….. (依据). 同理,PA=PC. ∴PA=PB=PC. ∴△PAB、△PBC、△PAC都是等腰三角形 |
任务:
A.请在图3中设计出一种裁剪方案,将该三角形纸片分成三个等腰三角形(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).
B.请在图3中设计出一种裁剪方案,将该三角形纸片分成四个等腰三角形,且四个三角形互不全等(要求:尺规作图,保留作图痕迹,不写作法,说明裁剪线).

问题情境:数学课上,同学们以等腰直角三角形为背景探究图形变化中的数学问题.如图1,将两张等腰直角三角形纸片重叠摆放在桌面,其中 ,
,
, 点A,D在
的同侧,点B,C在线段
上,连接
并延长
交
于点O,已知
. 将
从图1中的位置开始,绕点O顺时针旋转(
保持不动),旋转角为
.
请从下面A,B两题中任选一题作答.我选择 ▲ 题.
A.①猜想 ,
满足的数量关系,并说明理由;
②若 , 请直接写出
时,C,E两点间的距离;
B.①猜想 ,
满足的位置关系,并说明理由;
②若 , 请直接写出点F落在
延长线时,C,F两点间的距离.

问题情境
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
拓展探索
[动手操作]如图①,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AM,点B,E的对应点分别为B',E',展平纸片,连结AB',BB',BE'.请完成:

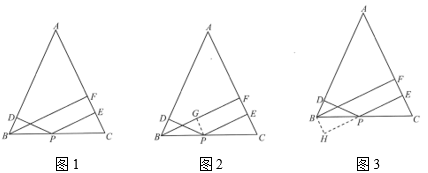
某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中,
, 点D、E分别是边
上的点,点P是底边
上的点,且
, 过点B作
于点F,请写出线段
、
、
之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交
的延长线于点H;
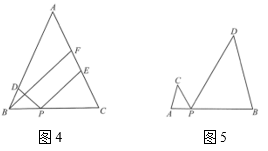
如图4,在等腰中,
, 点D、E分别是边
上的点,点P是底边
上的点,且
, 过点B作
交
于点F,请写出线段
之间满足的数量关系式,并说明理由.
如图5,在与
中,
,
, 点A、B、P在同一条直线上,若
,
, 则
.

②在图3中,作直线BD , CE交于点P , 直接写出当时旋转角
的度数.
勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法.如图.

把两个全等的直角三角形如图1放置,其三边长分别为 ,
,
. 显然,
,
. 请用
,
,
分别表示出梯形
, 四边形
,
的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
,
,
,则它们满足的关系式为,经化简,可得到勾股定理.
借助上面的思考过程,画图说明并求代数式的最小值
.
试题篮