命题新趋势7 阅读理解——2024年北师大版数学八（下）期末复习

1. 阅读下面材料：
在数学课上，老师提出如下问题：
已知：如图1， $\text{[math]}$ 及 $\text{[math]}$ 边的中点 $\text{[math]}$ ，求作：平行四边形 $\text{[math]}$ ．
小静的作法如下：
在数学课上，老师提出如下问题：
①连接 $\text{[math]}$ 并延长，在延长线上截取 $\text{[math]}$ ；
②连接 $\text{[math]}$ ．所以四边形 $\text{[math]}$ 就是所求作的平行四边形．
老师说：“小静的作法正确”．
请回答：小静的作法正确的理由是．

查看解析收藏纠错

+选题

2. 阅读与思考，同学们通过“真阅读工程”活动接触到很多课外阅读，其中有一段文章与勾股定理的内容相关：在直角坐标系中，已知两点的坐标是 $\text{[math]}$ ， $\text{[math]}$ ，求M、N两点之间的距离，可以通过 $\text{[math]}$ 变形为 $\text{[math]}$ 计算．
试根据以上知识解决下列问题：

（1）若点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 两点间的距离为；

（2）若点 $\text{[math]}$ 与 $\text{[math]}$ 的距离为10，求m的值；

（3）若点 $\text{[math]}$ ， $\text{[math]}$ ，点O是坐标原点，试判断 $\text{[math]}$ 是什么三角形，并说明理由．

查看解析收藏纠错

+选题
3. 先阅读下面的一段文字，再解答问题．
已知：在平面直角坐标系中，任意两点 $\text{[math]}$ ，其两点之间的距离公式为 $\text{[math]}$ ．同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点之间的距离公式可以简化为 $\text{[math]}$ 或 $\text{[math]}$ ．

（1）已知点 $\text{[math]}$ ，试求 $\text{[math]}$ 两点之间的距离．

（2）已知点 $\text{[math]}$ 在垂直于 $\text{[math]}$ 轴的直线上，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ， $\text{[math]}$ ，试确定点 $\text{[math]}$ 的坐标．

（3）已知点 $\text{[math]}$ ，请判断 $\text{[math]}$ 的形状，并说明理由．

查看解析收藏纠错

+选题
4. 阅读下列材料：
一般地，没有公因式的多项式，当项数为四项或四项以上时，经常把这些项分成若干组，然后各组运用提取公因式法或公式法分别进行分解，之后各组之间再运用提取公因式法或公式法进行分解，这种因式分解的方法叫做分组分解法．如：
因式分解： $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$ ．

（1）利用分组分解法分解因式：
$\text{[math]}$ ；
$\text{[math]}$

（2）因式分解： $\text{[math]}$ $\text{[math]}$ 直接写出结果 $\text{[math]}$ ．

查看解析收藏纠错

+选题
5. 阅读下列资料，解决问题：
定义：在分式中，对于只含有一个字母的分式，当分子的次数小于分母的次数时，我们称之为“真分式”，如： $\text{[math]}$ ，这样的分式就是真分式；当分子的次数大于或等于分母的次数时，我们称之为“假分式”，如： $\text{[math]}$ 这样的分式就是假分式，假分式也可以化为带分式（即：整式与真分式的和的形式）．
如： $\text{[math]}$ ．

（1）分式 $\text{[math]}$ 是（填“真分式”或“假分式”）；

（2）将假分式 $\text{[math]}$ 分别化为带分式；

（3）如果分式 $\text{[math]}$ 的值为整数，求所有符合条件的整数x的值．

查看解析收藏纠错

+选题
6. 阅读与思考：分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式，比如：四项的多项式一般按照“两两”分组或“三一”分组，进行分组分解.
例1：“两两分组”： $\text{[math]}$
解：原式 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
例2：“三一分组”： $\text{[math]}$
解：原式 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
归纳总结：用分组分解法分解因式要先恰当分组，然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下，解答下列问题：

（1）分解因式：
① $\text{[math]}$ ；
② $\text{[math]}$ .

（2）已知 $\text{[math]}$ 的三边a ， b ， c满足 $\text{[math]}$ ，试判断 $\text{[math]}$ 的形状.

查看解析收藏纠错

+选题
7. 阅读理解：对于线段 $\text{[math]}$ 和点 $\text{[math]}$ ，定义：若 $\text{[math]}$ ，则称点 $\text{[math]}$ 为线段 $\text{[math]}$ 的“等距点”；特别地，若 $\text{[math]}$ ，则称点 $\text{[math]}$ 是线段 $\text{[math]}$ 的“完美等距点”．
解决问题：如图，在平面直角坐标系中， $\text{[math]}$ 为坐标原点，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上一动点．

（1）已知3个点： $\text{[math]}$ 则线段 $\text{[math]}$ 的“等距点”是______，线段 $\text{[math]}$ 的“完美等距点”是______；

（2）若 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且 $\text{[math]}$ 是线段 $\text{[math]}$ 的“等距点”，求点 $\text{[math]}$ 的坐标；

（3）当 $\text{[math]}$ ，是否存在这样的点 $\text{[math]}$ ，使点 $\text{[math]}$ 是线段 $\text{[math]}$ 的“等距点”且为线段 $\text{[math]}$ 的“完美等距点”，请直接写出所有这样的点P的坐标．

查看解析收藏纠错

+选题

8. 阅读与思考：下面是小宇同学的数学日记，请仔细阅读并完成相应的任务．

×年×月×日星期日

用等面积法解决问题

周末，我对本学期所学的内容进行了回顾与整理，发现数学中有许多方法是可以互相迁移的．

比如我们在学习整式乘法时，借助如图1所示的边长为 $\text{[math]}$ 的正方形，用两种不同的方法表示这个正方形的面积，可以得到乘法公式 ① ．

再比如学习三角形的内容时，我遇到了同样可以用等面积法解决的问题．如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求点 $\text{[math]}$ 到 $\text{[math]}$ 的距离．我们也可以利用等面积法求得点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为 ② ．

总结：等面积法是一种重要的数学解题方法，在解题中，灵活运用等面积法解决相关问题，不仅可以使解题思路清晰，过程简洁，而且还能体现知识间的相互联系．

任务：

（1）请你补全小宇日记中不完整的部分：①__________，②__________．

（2）尺规作图：在图2中作 $\text{[math]}$ 的角平分线，交 $\text{[math]}$ 于点 $\text{[math]}$ （保留作图痕迹，不写作法）．

（3）在（2）的条件下，求线段 $\text{[math]}$ 的长度．

查看解析收藏纠错

+选题

9. 先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式 $\text{[math]}$ .

解∵ $\text{[math]}$ ， ∴ $\text{[math]}$ ，可化为 $\text{[math]}$ .

由有理数的乘法法则：两数相乘，同号得正，得：① $\text{[math]}$ ， ② $\text{[math]}$

解不等式组①，得 $\text{[math]}$ ，解不等式组②，得 $\text{[math]}$ ，

∴ $\text{[math]}$ 的解集为 $\text{[math]}$ 或 $\text{[math]}$

即一元二次不等式 $\text{[math]}$ 的解集为x>2或 $\text{[math]}$ .

（1）一元二次不等式 $\text{[math]}$ 的解集为；

（2）试解一元二次不等式 $\text{[math]}$ ；

（3）试解不等式 $\text{[math]}$ .

查看解析收藏纠错

+选题

10. 阅读与思考，请阅读下列材料，并完成相应的任务．

旋转对称图形

观察右图中的正六边形，点O是它的内角平分线的交点，将这个正六边形绕着点O旋转 $\text{[math]}$ ，旋转后的图形与旋转前的图形重合．

一般地，如果把一个图形绕着某一点旋转一定角度（小于 $\text{[math]}$ ）后，能够与原来的图形重合，那么这个图形叫做旋转对称图形，这个点叫它的对称中心．

（1）中心对称图形旋转对称图形．（填“是”或“不是”）

（2）下列图形中不是旋转对称图形的有，既是旋转对称图形又是中心对称图形的有，旋转72°能够完全重合的图形有．

A． B． C． D． E．

查看解析收藏纠错

+选题

11. 阅读理解：已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 试比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小．
想法：求 $\text{[math]}$ 当 $\text{[math]}$ ，则 $\text{[math]}$ ；当 $\text{[math]}$ ，则 $\text{[math]}$ ；当 $\text{[math]}$ ，则 $\text{[math]}$ ．
解： $\text{[math]}$ ， $\text{[math]}$ ．
用你学到的方法解决下列问题：

（1）已知 $\text{[math]}$ 且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 试比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小．

（2）甲、乙两地相距 $\text{[math]}$ ，小明和小宇同路往返于甲乙两地．小明去时和返回时的速度分别是 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ；小宇去时和返回时的速度都是 $\text{[math]}$ 请问二者一个来回中，谁用时更短？

查看解析收藏纠错

+选题
12. 阅读与思考
请阅读下列材料，并完成相应的任务．
$\text{[math]}$ 年 $\text{[math]}$ 月 $\text{[math]}$ 日星期一
今天，同学们学习了三角形中位线定理的相关内容，知道了“三角形的中位线平行于第三边，且等于第三边的一半”．课下，对三角形中位线定理的相关知识进行了复习，并对它相关的命题产生了兴趣．如图1，在 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 边上的点，同学们提出了以下三个命题：

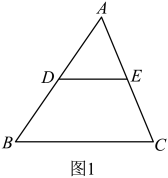
I.若 $\text{[math]}$ 是 $\text{[math]}$ 边的中点，且 $\text{[math]}$ ，则 $\text{[math]}$ 是 $\text{[math]}$ 边的中点．
II.若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 分别是 $\text{[math]}$ 边的中点．
III.若 $\text{[math]}$ 是 $\text{[math]}$ 边的中点，且 $\text{[math]}$ ，则 $\text{[math]}$ 是 $\text{[math]}$ 边的中点．
任务：

（1）从所提出的三个命题中选择一个假命题，并在图2中画出反例．（要求：尺规作图，保留作图痕迹）

（2）从所提出的三个命题中选择一个真命题进行证明．

查看解析收藏纠错

+选题
13. 阅读下面材料：
小明遇到这样一个问题：如图1，在△ABC中，DE//BC，分别交AB，AC于点D，E，已知CD⊥BE，CD=3，BE=5，求BC+DE的值.
小明发现，过点E作EF//DC，交BC延长线于点F，构造△BEF，经过推理和计算能够使问题得到解决（如图2）.

（1）请回答：BC+DE的值为；

（2）参考小明思考的问题的方法，解决问题：如图3，▱ABCD中，E是BC的中点，AE=9，BD=12，AD=10，求证：AE⊥BD.

查看解析收藏纠错

+选题
14. 阅读与思考
若两个等腰三角形有公共腰，则称这两个等腰三角形不在公共腰上的两个顶点关于腰互为对顶点．若再满足不在公共腰上的两个角的和是90°，则称这两个顶点关于腰为互余对顶点．

如图1，在四边形ABCD中，AC是一条对角线，CD=CA=CB，则点B与点D关于AC互为对顶点，若再满足∠B+∠D=90°，则点B与点D关于AC为互余对顶点．

任务：

如图2，平行四边形ABCD与四边形ABCE有两边重合，AC为两个四边形的对角线，AE=AD=AC，∠ACB=70°．

（1）证明：点B与点E关于AC互为对顶点．

（2）当点B与点E关于AC为互余对顶点时，求∠DCE的度数．

查看解析收藏纠错

+选题
15. 请阅读下列材料，完成相应的任务：
无刻度直尺作图：“无刻度直尺”是尺规作图的工具之一，它的作用在于连接任意两点、作任意直线、延长任意线段．结合图形的性质，只利用无刻度直尺也可以解决一些几何作图问题．
如图1，已知点P是线段AB的中点，分别以PA、PB为边在AB的同侧作 $\text{[math]}$ 与 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求作：线段PC的中点E．
按照常规思路，用尺规作线段PC的垂直平分线，垂足即为PC的中点．仔细分析图形，你会发现，只用无刻度的直尺连接线段AD，AD与CP交点E即为PC的中点（如图2）．
证明：连接CD．
$\text{[math]}$ ，
$\text{[math]}$ （依据1），
$\text{[math]}$ ，
$\text{[math]}$ ，同理， $\text{[math]}$ ．
……

（1）【任务1】写出上述证明过程中依据1的内容：．

（2）【任务2】请补全证明过程．

（3）【任务3】如图，在平行四边ABCD中，点E是CD边的中点．求作： $\text{[math]}$ ，使 $\text{[math]}$ 的面积与平行四边ABCD的面积相等．（要求：利用无刻度直尺作图，保留作图痕迹，不写画法．）

查看解析收藏纠错

+选题
16. 阅读下面材料，并解决问题：

（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
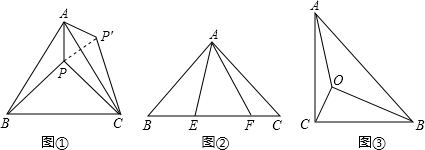
为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB＝；

（2）基本运用
请你利用第（1）题的解答思想方法，解答下面问题：

已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF²＝BE²+FC²；

（3）能力提升
如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．

查看解析收藏纠错

+选题
17. 阅读情境：在综合实践课上，同学们探究“全等的等腰直角三角形图形变化问题”．
如图1， $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ，此时，点 $\text{[math]}$ 与点 $\text{[math]}$ 重合．

（1）操作探究1：小凡将图1中的两个全等的 $\text{[math]}$ 和 $\text{[math]}$ 按图2方式摆放，点 $\text{[math]}$ 落在 $\text{[math]}$ 上， $\text{[math]}$ 所在直线交 $\text{[math]}$ 所在直线于点 $\text{[math]}$ ，连结 $\text{[math]}$ ，求证： $\text{[math]}$ ．

（2）操作探究2：小彬将图1中的 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转角度 $\text{[math]}$ ，然后，分别延长 $\text{[math]}$ 、 $\text{[math]}$ ，它们相交于点 $\text{[math]}$ ．如图3，在操作中，小彬提出如下问题，请你解答：
① $\text{[math]}$ 时，求证： $\text{[math]}$ 为等边三角形；

②当 $\text{[math]}$ 时， $\text{[math]}$ ．（直接回答即可）

（3）操作探究3：小颖将图1中的 $\text{[math]}$ 绕点A按顺时针方向旋转角度 $\text{[math]}$ ，线段 $\text{[math]}$ 和 $\text{[math]}$ 相交于点 $\text{[math]}$ ，当旋转到点 $\text{[math]}$ 是边 $\text{[math]}$ 的中点时（可利用图4画图），直接写出线段 $\text{[math]}$ 的长为．

查看解析收藏纠错

+选题
18. 请阅读下列材料：已知：如图（1）在 $\text{[math]}$ 中， $\text{[math]}$ ，点D、E分别为线段 $\text{[math]}$ 上两动点，若 $\text{[math]}$ .探究线段 $\text{[math]}$ 三条线段之间的数量关系.小明的思路是：把 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，使问题得到解决.请你参考小明的思路探究并解决下列问题：

（1）猜想 $\text{[math]}$ 三条线段之间存在的数量关系式，直接写出你的猜想；

（2）当动点E在线段 $\text{[math]}$ 上，动点D运动在线段 $\text{[math]}$ 延长线上时，如图（2），其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明；

（3）已知：如图（3），等边三角形 $\text{[math]}$ 中，点D、E在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，请你找出一个条件，使线段 $\text{[math]}$ 能构成一个等腰三角形，并求出此时等腰三角形顶角的度数.

查看解析收藏纠错

+选题
19. 阅读下面的解题过程：
已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
解：由已知可得 $\text{[math]}$ ，则 $\text{[math]}$ ，即 $\text{[math]}$ ．
$\text{[math]}$ ，
$\text{[math]}$ ．
上面材料中的解法叫做“倒数法”．
请你利用“倒数法”解下面的题目：

（1）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

（2）已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题

20. 下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段，请仔细阅读，并完成相应的任务．

小明：如图1，⑴分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上截取 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ 不重合）；⑵分别作线段 $\text{[math]}$ ， $\text{[math]}$ 的垂直平分线 $\text{[math]}$ ， $\text{[math]}$ ，交点为 $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ ；

⑶作射线 $\text{[math]}$ ，射线 $\text{[math]}$ 即为 $\text{[math]}$ 的平分线．

简述理由如下：

由作图知， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ ，则 $\text{[math]}$ ，即射线 $\text{[math]}$ 是 $\text{[math]}$ 平分线．

小军：我认为小明的作图方法很有创意，但是太麻烦了，可以改进如下，如图2，

⑴分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上截取 $\text{[math]}$ ， $\text{[math]}$ （点C，E不重合）；⑵连接 $\text{[math]}$ ， $\text{[math]}$ ，交点为P；（3）作射线 $\text{[math]}$ ．射线 $\text{[math]}$ 即为 $\text{[math]}$ 的平分线．

……

任务：

（1）小明得出 $\text{[math]}$ 的依据是（填序号）．

① $\text{[math]}$ ② $\text{[math]}$ ③ $\text{[math]}$ ④ $\text{[math]}$ ⑤ $\text{[math]}$

（2）小军作图得到的射线 $\text{[math]}$ 是 $\text{[math]}$ 的平分线吗？请判断并说明理由．

（3）如图3，已知 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别为射线 $\text{[math]}$ ， $\text{[math]}$ 上的点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，交点为 $\text{[math]}$ ，当 $\text{[math]}$ 时，请直接写出 $\text{[math]}$ 的度数．

查看解析收藏纠错

+选题

21. 请阅读求绝对值不等式|x|＜3和|x|＞3的解集的过程：
因为|x|＜3，从如图1所示的数轴上看：大于-3而小于3的数的绝对值是小于3的，所以|x|＜3的解集是-3＜x＜3；
因为|x|＞3，从如图2所示数轴上看：小大于-3的数和大于3的数的绝对值是大于3的，所以|x|＞3的解集是x＜-3或x＞3．
解答下面的问题：

（1）不等式|x|＜a（a＞0）的解集为；不等式|x|＞a（a＞0）的解集为．

（2）解不等式|x-5|＜3；

（3）解不等式|x-3|＞5．

查看解析收藏纠错

+选题
22. 【阅读】根据等式和不等式的基本性质，我们可以得到比较两数大小的方法：
若 $\text{[math]}$ ，则 $\text{[math]}$ ；

若 $\text{[math]}$ ，则 $\text{[math]}$ ；

若 $\text{[math]}$ ，则 $\text{[math]}$ .

反之也成立.

这种比较大小的方法称为“作差法比较大小”.

（1）【理解】若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”、“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）

（2）【运用】若 $\text{[math]}$ ， $\text{[math]}$ ，试比较 $\text{[math]}$ ， $\text{[math]}$ 的大小.

（3）【拓展】请运用“作差法比较大小”解决下面这个问题.制作某产品有两种用料方案，方案一：用5块A型钢板，6块 $\text{[math]}$ 型钢板.方案二：用4块A型钢板，7块 $\text{[math]}$ 型钢板.每块A型钢板的面积比每块 $\text{[math]}$ 型钢板的面积小.方案一的总面积记为 $\text{[math]}$ ，方案二的总面积记为 $\text{[math]}$ ，试比较 $\text{[math]}$ ， $\text{[math]}$ 的大小.

查看解析收藏纠错

+选题
23. 【阅读理解】我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，解决此类问题时一般要进行转化，其中“作差法”就是常用的方法之一．其依据是不等式（或等式）的性质：若 $\text{[math]}$ ，则 $\text{[math]}$ ；若 $\text{[math]}$ ，则 $\text{[math]}$ ；若 $\text{[math]}$ ，则 $\text{[math]}$ ．
例：已知 $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ ，求证： $\text{[math]}$

证明： $\text{[math]}$

$\text{[math]}$

$\text{[math]}$ ，故 $\text{[math]}$

（1）【新知理解】比较大小： $\text{[math]}$ $\text{[math]}$ ．（填“ $\text{[math]}$ ”，“＝”，“ $\text{[math]}$ ”）

（2）【问题解决】甲、乙两个平行四边形，其底和高如图所示（ $\text{[math]}$ 为正整数），其面积分别为 $\text{[math]}$ ， $\text{[math]}$ ．请比较 $\text{[math]}$ ， $\text{[math]}$ 的大小关系．

（3）【拓展应用】请用“作差法”解决下列问题：
某游泳馆在暑假期间对学生优惠开放，有A，B两种方案可供选择，A方案：每次按原价打9折收费；B方案：前5次按照原价收费，从第6次起每次打8折．请问游泳的学生选择哪种方案更合算？

查看解析收藏纠错

+选题
24. 阅读以下材料：
因式分解： $\text{[math]}$ ，

解：令 $\text{[math]}$ ，则原式： $\text{[math]}$ ，

再将“A”还原，得原式 $\text{[math]}$ ，

上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请你解答下列问题：

（1）因式分解： $\text{[math]}$ ；

（2）当n为何值时，代数式 $\text{[math]}$ 有最小值？最小值为多少？

查看解析收藏纠错

+选题
25. 阅读下面的材料：把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例：将分式 $\text{[math]}$ 表示成部分分式，解：设 $\text{[math]}$ ，将等式右边通分，得 $\text{[math]}$ ，依据题意，得 $\text{[math]}$ ，解得 $\text{[math]}$ ，所以 $\text{[math]}$ 请你适用上面所学到的方法，解决下面的问题：

（1） $\text{[math]}$ （A ， B为常数），则 $\text{[math]}$ ， $\text{[math]}$ ；

（2）一个容器装有 $\text{[math]}$ 水，按照如下要求把水倒出：第1次倒出 $\text{[math]}$ 水，第2次倒出的水量是 $\text{[math]}$ 的 $\text{[math]}$ ，第3次倒出的水量是 $\text{[math]}$ 的 $\text{[math]}$ ，第4次倒出的水量是 $\text{[math]}$ 的 $\text{[math]}$ …第n次倒出的水量是 $\text{[math]}$ 的 $\text{[math]}$ …按照这种倒水的方法，这 $\text{[math]}$ 的水是否能倒完？如果能，多少次能倒完？如果不能，请说明理由；

（3）按照（2）的条件，现在开始重新实验，按照如下要求把水倒出：第1次倒出 $\text{[math]}$ 水，第2次倒出的水量是 $\text{[math]}$ ，第3次倒出的水量是 $\text{[math]}$ ，第4次倒出的水量是 $\text{[math]}$ ，请问经过多少次操作后，杯内剩余水量能否变成原来水量的 $\text{[math]}$ ？试说明理由.

查看解析收藏纠错

+选题

命题新趋势7 阅读理解——2024年北师大版数学八（下）期末复习

一、填空题

二、解答题

三、综合题

四、实践探究题

相关试卷收起∨

命题新趋势7 阅读理解——2024年北师大版数学八（下）期末复习

一、填空题

二、解答题

三、综合题

四、实践探究题

相关试卷 收起∨

相关试卷收起∨