2024年浙教版数学八（下）微素养核心突破24 反比例函数与一次函数综合

1. 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于A，B两点，点A的横坐标为2，点B的横坐标为 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，反比例函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ， $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或x＞2 D . $\text{[math]}$ 或 $\text{[math]}$

查看解析收藏纠错

+选题
3. 在平面直角坐标系xOy中，直线AB垂直于x轴于点C(点C在原点的右侧)，并分别与直线y=x和双曲线y= $\text{[math]}$ 相交于点A，B，且AC+BC=4，则△OAB的面积为（）

A . 2+ $\text{[math]}$ 或2- $\text{[math]}$ B . 2 $\text{[math]}$ +2或2 $\text{[math]}$ -2 C . 2- $\text{[math]}$ D . 2 $\text{[math]}$ +2

查看解析收藏纠错

+选题
4. 如图，反比例函数 $\text{[math]}$ 和正比例函数 $\text{[math]}$ 的图象相交于A(-1，-3)，B(1，3)两点.若 $\text{[math]}$ 则x的取值范围是（）

A . $\text{[math]}$ 1<x<0 B . $\text{[math]}$ 1<x<1 C . x< $\text{[math]}$ 1或0<x<1 D . $\text{[math]}$ 1<x<0或x>1

查看解析收藏纠错

+选题
5. 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数 $\text{[math]}$ 的图象上，点D的坐标为(4，3).若将菱形ABCD沿x轴正方向平移，则当菱形的顶点D落在函数 $\text{[math]}$ 的图象上时，菱形ABCD沿x轴正方向平移的距离为（）

A . 3 B . 5 C . $\text{[math]}$ D . 8

查看解析收藏纠错

+选题
6. 如图，一次函数y=ax+b(a≠0)与反比例函数y $\text{[math]}$ 的图象相交于点A(1，2)，B(m，-1)，则关于x的不等式 $\text{[math]}$ 的解是（）

A . x<-2或0<x<1 B . x<-1或0<x<2 C . -2<x<0或x>1 D . -1<x<0或x>2

查看解析收藏纠错

+选题
7. 函数 $\text{[math]}$ 和y=-kx+2(k≠0)；在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 已知关于x的一元二次方程 $\text{[math]}$ ，及函数 $\text{[math]}$ ， $\text{[math]}$ （a，b，c为常数，且 $\text{[math]}$ ），则（）

A . 若方程 $\text{[math]}$ 有解，则函数 $\text{[math]}$ 的图象一定有交点 B . 若方程 $\text{[math]}$ 有解，则函数 $\text{[math]}$ 的图象一定没有交点 C . 若方程 $\text{[math]}$ 无解，则函数 $\text{[math]}$ 的图象一定有交点 D . 若方程 $\text{[math]}$ 无解，则函数 $\text{[math]}$ 的图象一定没有交点

查看解析收藏纠错

+选题
9. 反比例函数 $\text{[math]}$ 图像上有两个点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的图像不经过第（）象限

A . 一 B . 二 C . 三 D . 四

查看解析收藏纠错

+选题
10. 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图像相交于A、B两点，与x轴，y轴分别相交于C、D两点，连接OA、OB．过点A作 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．设点A的横坐标为 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . $\text{[math]}$ C . 2 D . 4

查看解析收藏纠错

+选题

11. 如图，在平面直角坐标系中，直线y₁=k₁x+b与双曲线y₂= $\text{[math]}$ (其中k₁ ， k₂≠0)相交于A(-2，3)，B(m，-2)两点，过点B作BP∥x轴，交y轴于点P，则△ABP的面积是

查看解析收藏纠错

+选题
12. 如图，矩形ABCD的边AB与y轴平行，已知点A(1，m)，C(3，m+6)，则图象同时经过点B与点D的反比例函数的表达式为.

查看解析收藏纠错

+选题
13. 若在反比例函数 $\text{[math]}$ 的图象的每一分支上，y都随x的增大而减小，且整式 $\text{[math]}$ 是一个完全平方式，则该反比例函数的表达式为.

查看解析收藏纠错

+选题
14. 如图，正比例函数：y=ax(a≠0)的图象与反比例函数 $\text{[math]}$ 的图象相交于点A，B.若点A的坐标为( $\text{[math]}$ 2，3)，则点B的坐标为.

查看解析收藏纠错

+选题
15. 如图，一次函数 $\text{[math]}$ ( $\text{[math]}$ 和 $\text{[math]}$ 均为常数且 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 为常数且 $\text{[math]}$ 的图象交于A，B两点，其横坐标分别为1和2.5，则关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集是.

查看解析收藏纠错

+选题
16. 如图，在平面直角坐标系xOy中，直线y=kx(k <0)与反比例函数 $\text{[math]}$ 的图象相交于A，C两点，D为x轴负半轴上一点，连结CD 并延长，交反比例函数 $\text{[math]}$ 的图象于点B.若CB =2CD，△CDO的面积为1，则m-n=.

查看解析收藏纠错

+选题

17. 已知：如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，

（1）求 $\text{[math]}$ 的值及点 $\text{[math]}$ 的坐标；

（2）写出 $\text{[math]}$ 时 $\text{[math]}$ 的取值范围；

（3） $\text{[math]}$ 是 $\text{[math]}$ 轴上一点，且满足 $\text{[math]}$ 的面积等于 $\text{[math]}$ .求点 $\text{[math]}$ 坐标.

查看解析收藏纠错

+选题
18. 如图，四边形ABCD的四个顶点分别在反比例函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象上，对角线BD∥y轴，且BD⊥AC于点P.已知点B的横坐标为4.

（1）当m=4，n=20时，
①若点P的纵坐标为2，求直线AB的函数表达式.
②若P是BD的中点，试判断四边形ABCD的形状，并说明理由.

（2）四边形ABCD能否为正方形?若能，求此时m，n之间的数量关系；若不能，请说明理由.

查看解析收藏纠错

+选题
19. 已知一次函数y=2x-1和反比例函数 $\text{[math]}$ 的图象的一个交点的坐标为(1，a).

（1）求反比例函数的表达式.

（2）若这两个函数图象的另一个交点为A，求点A的坐标.

（3）在(2)的条件下，若点B的坐标为(2，0)，且以A，O，B，P为顶点的四边形是平行四边形，请你直接写出点P的坐标.

查看解析收藏纠错

+选题
20. 如图，在平面直角坐标系中，已知一次函数 $\text{[math]}$ 的图象与坐标轴分别相交于A(5，0)，B.(0， $\text{[math]}$ )两点，且与反比例函数 $\text{[math]}$ 的图象在第一象限内相交于P，K两点，连结OP，△OAP的面积为 $\text{[math]}$ .

（1）求一次函数与反比例函数的表达式.

（2）当y₂>y₁时，求x的取值范围.

（3）若C为线段OA上的一个动点，当PC+KC的值最小时，求△PKC的面积.

查看解析收藏纠错

+选题
21. 如图，在平面直角坐标系 xOy中，一次函数y =ax+b(a≠0)的图象与反比例函数 $\text{[math]}$ ≠0)的图象相交于 P，Q两点，点 P(-4，3)，点 Q 的纵坐标为-2.求：

（1）反比例函数与一次函数的表达式.

（2） △POQ的面积.

查看解析收藏纠错

+选题
22. 已知一次函数y=kx+b(k≠0)的图象与反比例函数 $\text{[math]}$ 的图象相交于点A(1，m)，B(n，-2).

（1）求一次函数的表达式，并在如图所示的直角坐标系中画出这个一次函数的图象.

（2）根据(1)中的函数图象，直接写出不等式 $\text{[math]}$ 的解.

（3）若点 C 是点 B 关于 y 轴的对称点，连结AC，BC，求△ABC的面积.

查看解析收藏纠错

+选题
23. 如图，菱形 $\text{[math]}$ 的边 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点A的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

（1）求 $\text{[math]}$ 的值．

（2）求 $\text{[math]}$ 的面积．

（3）已知点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围为．

查看解析收藏纠错

+选题
24. 如图，正比例函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象都经过点 A(a，2).

（1）求点 A 的坐标和反比例函数的表达式.

（2）若点 P(m，n)在该反比例函数的图象上，且它到 y轴的距离小于 3，请根据图象直接写出 n的取值范围.

查看解析收藏纠错

+选题
25. 如图，一次函数图象与反比例函数图象交于点A(-1，6)，B( $\text{[math]}$ ， a-3)，与x轴交于点C，与y轴交于点D．

（1）求反比例函数与一次函数的表达式；

（2）点M在x轴上，若S_△_O_AM=S_△_O_AB ，求点M的坐标．

查看解析收藏纠错

+选题
26. 设函数 $\text{[math]}$ 函数 $\text{[math]}$ （k₁、k₂、b是常熟，k₁≠0，k₂≠0）.

（1）若函数y₁和函数 y₂的图象相交于点 A (1，m)，B(3，1)，
①求函数 y₁，y₂ 的表达式.
②当2<x<3时，比较 y₁ 与y₂的大小（直接写出结果）.

（2）若点 C（2，n）在函数 y₁ 的图像上，点 C 先向下平移 2个单位，再向左平移4 个单位，得点D.若点 D 恰好落在函数 y₁ 的图像上，求 n 的值.

查看解析收藏纠错

+选题

27. 阅读材料：
已知：一次函数y＝﹣x+b与反比例函数y＝ $\text{[math]}$ （x＞0），当两个函数的图象有交点时，求b的取值范围.

（1）方方给出了下列解答：
﹣x+b＝ $\text{[math]}$

x²﹣bx+4＝0

∵两个函数有交点

∴△＝b²﹣16≥0

但是方方遇到了困难：利用已学的知识无法解b²﹣16≥0这个不等式；

此时，圆圆提供了另一种解题思路；

第1步：先求出两个函数图象只有一个交点时，b＝ ▲ ；

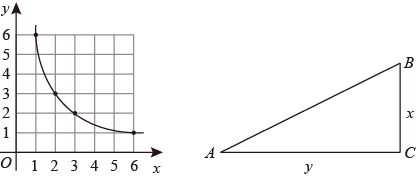
第2步：画出只有一个交点时两函数的图象（请帮圆圆在直角坐标系中画出图象）；

第3步：通过平移y＝﹣x+b的图象，观察得出两个函数的图象有交点时b的取值范围是 ▲ .

应用：

如图，Rt△ABC中，∠C＝90°，BC的长为x，AC的长为y，且S_△ABC＝12.

（2）求y关于x的函数表达式；

（3）设x+y＝m，求m的取值范围.

查看解析收藏纠错

+选题

2024年浙教版数学八（下）微素养核心突破24 反比例函数与一次函数综合

一、选择题

二、填空题

三、综合题

四、实践探究题

相关试卷收起∨

2024年浙教版数学八（下）微素养核心突破24 反比例函数与一次函数综合

一、选择题

二、填空题

三、综合题

四、实践探究题

相关试卷 收起∨

相关试卷收起∨