2024年广东省中考数学全真模拟试卷(一)

修改时间：2024-05-30 浏览次数：179 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. $\text{[math]}$ 的绝对值是（）

A . 2024 B . $\text{[math]}$ C . $\text{[math]}$ D . 0

查看解析收藏纠错

+选题
2. 下列是围绕2022年北京冬奥会设计的剪纸图案，其中既是中心对称图形又是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 经历百年风雨，中国共产党从小到大、由弱到强，从建党时 $\text{[math]}$ 多名党员，发展成为今天已经拥有超过 $\text{[math]}$ 万党员的世界第一大政党． $\text{[math]}$ 万用科学记数法表示为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板)，其依据是（）

A . 同旁内角互补，两直线平行 B . 两直线平行，同旁内角互补 C . 同位角相等，两直线平行 D . 两直线平行，同位角相等

查看解析收藏纠错

+选题
5. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. “二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”，小兰购买了四张“二十四节气”主题邮票，其中“立春”有两张，“雨水”和“惊垫”各一张，从中随机抽取一张恰好抽到“立春”概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 柏拉图借毕达哥拉斯主义者提马尤斯门（Timaeus）的口说出以下的话：“两个东西不可能有完美的结合，除非另有第三者存在其间，因为他们之间必须有一种结合物，最好的结合物是比例．设有三个数量，若中数与小数之比等于大数与中数之比，反过来，小数与中数之比等于中数与大数之比﹣﹣则后项就是前项和中数，中数就是前项和后项，所以三者必然相同，即为相同，就是一体”请问柏拉图在谈论的是什么数学概念，这个数学概念中涉及到的一个实数是什么？（　　）

A . 圆周率π B . 勾股定理（毕达哥拉斯定理） 3：4：5 C . 黄金分割 $\text{[math]}$ D . 黄金密度19.8千克/立方米

查看解析收藏纠错

+选题
8. 如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连接OD，若∠C=50°，则∠AOD的度数为（）

A . 40° B . 50° C . 70° D . 80°

查看解析收藏纠错

+选题
9. 如图，在平面直角坐标系中，O是坐标原点，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点C，点A在反比例函数 $\text{[math]}$ 的图象上，若 $\text{[math]}$ ， $\text{[math]}$ ，则k的值为（）．

A . 12 B . 8 C . 6 D . 3

查看解析收藏纠错

+选题
10. 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ 为BC中点. $\text{[math]}$ 为AB上一点， $\text{[math]}$ ， CE和AD相交于点 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题：本大题共5小题，每小题3分，共15分．

11. 因式分解： $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 某公司今年一月盈利30万元，三月盈利36.3万元，从一月到三月，每月盈利的增长率都相同，设月平均增长率为x ，根据题意可列方程为．

查看解析收藏纠错

+选题
13. 已知一个n边形的内角和等于720°，则n=．

查看解析收藏纠错

+选题
14. 某施工队要铺设一段全长2000米的管道，中考期间需停工两天，实际施工时，每天需比原来计划多铺设50米，才能按时完成任务，求原计划每天施工多少米，设原计划每天施工x米，则根据题意可列方程为.

查看解析收藏纠错

+选题
15. 在直角 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 内一点，满足 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为.

查看解析收藏纠错

+选题

三、解答题(一)：本大题共3小题，第16题10分，第17、18题各7分，共24分．

16.

（1）解一元一次不等式组 $\text{[math]}$ ；

（2）已知一次函数的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ，求这个函数的解析式．

查看解析收藏纠错

+选题
17. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．

（1）实践与操作：请用尺规作图的方法在线段 $\text{[math]}$ 上找点 $\text{[math]}$ ，使得 $\text{[math]}$ ；（保留作图痕迹，不要求写作法）

（2）应用与计算：在（1）的条件下，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
18. 某社区积极响应正在开展的“创文活动”，安排甲、乙两个工程队对社区进行绿化改造．已知甲工程队每天能完成的绿化改造面积是乙工程队每天能完成的绿化改造面积的2倍，且甲工程队完成 $\text{[math]}$ 的绿化改造比乙工程队完成 $\text{[math]}$ 的绿化改造少用4天．分别求甲、乙两工程队每天能完成绿化改造的面积．

查看解析收藏纠错

+选题

四、解答题(二)：本大题共3小题，每小题9分，共27分．

19. 某中学为了解九年级学生的体能状况，从九年级学生中随机抽取部分学生进行体能测试，测试结果分为A ， B ， C ， D四个等级．请根据两幅统计图中的信息回答下列问题：

（1）本次抽样调查共抽取了名学生．

（2）求测试结果为C等级的学生数，并补全条形图；

（3）若该中学九年级共有600名学生，请你估计该中学九年级学生中体能测试结果为 $\text{[math]}$ 等级的学生有多少名？

（4）若从体能为 $\text{[math]}$ 等级的2名男生2名女生中随机的抽取2名学生，作为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是女生的概率．

查看解析收藏纠错

+选题
20. 如图，已知点E在平行四边形ABCD边DA延长线上，且AE=AD．求证：四边形AEBC是平行四边形．

查看解析收藏纠错

+选题
21. 【项目化学习】
项目主题：从函数角度重新认识“阻力对物体运动的影响”．
项目内容：数学兴趣小组对一个静止的小球从斜坡滚下后，在水平木板上运动的速度、距离与时间的关系进行了深入探究，兴趣小组先设计方案，再进行测量，然后根据所测量的数据进行分析，并进一步应用。
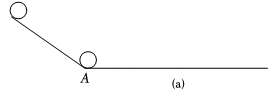
实验过程：如图（a）所示，一个黑球从斜坡顶端由静止滚下沿水平木板直线运动，从黑球运动到点A处开始，用频闪照相机、测速仪测量并记录黑球在木板上的运动时间x（单位：s）、运动速度v（单位：cm/s）、滑行距离y（单位：cm）的数据．
任务一：数据收集
记录的数据如下：
运动时间x/s
0
2
4
6
8
10
…
运动速度v/（cm/s）
10
9
8
7
6
5
…
滑行距离y/cm
0
19
36
51
64
75
…
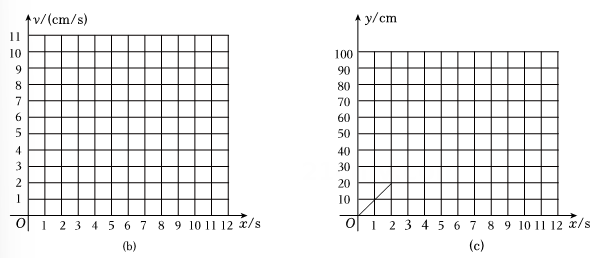
根据表格中的数值分别在图（b）、图（c）中作出v与x的函数图象、y与x的函数图象：

（1）请在图（b）中画出v与x的函数图象：

（2）【任务二：观察分析】数学兴趣小组通过观察所作的函数图象，并结合已学习过的函数知识，发现图（b）中v与x的函数关系为一次函数关系，图（c）中y与x的函数关系为二次函数关系．请你结合表格数据，分别求出v与x的函数关系式和y与x的函数关系式：（不要求写出自变量的取值范围）

（3）【任务三：问题解决】当黑球在水平木板停下来时，求此时黑球的滑行距离：

（4）若黑球到达木板点A处的同时，在点A的前方 $\text{[math]}$ 处有一辆电动小车，以2cm/s的速度匀速向右直线运动，若黑球不能撞上小车，则n的取值范围应为．

查看解析收藏纠错

+选题

五、解答题(三)：本大题共2小题，每小题12分，共24分．

22. 综合探究
如图1， $\text{[math]}$ 是 $\text{[math]}$ 的内接三角形， $\text{[math]}$ 是 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，满足 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ．

（2）求证： $\text{[math]}$ ．

（3）如图2， $\text{[math]}$ 为 $\text{[math]}$ 的直径，设 $\text{[math]}$ ，当 $\text{[math]}$ 的长为2时，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
23. 定义：对角线互相垂直且相等的四边形叫做垂等四边形．

（1）理解应用：如图1，在平面直角坐标系 $\text{[math]}$ 中，已知四边形 $\text{[math]}$ 是垂等四边形，点A的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ，则点B的坐标为．

（2）综合探究：如图2，已知抛物线 $\text{[math]}$ 与x轴交于A ， B两点，点A在点B的左侧，C ， D两点在该抛物线上．若以A ， B ， C ， D为顶点的四边形是垂等四边形，设点C的横坐标为m ，点D的横坐标为n ，且 $\text{[math]}$ ，求m的值．

查看解析收藏纠错

+选题

运动时间x/s	0	2	4	6	8	10	…
运动速度v/（cm/s）	10	9	8	7	6	5	…
滑行距离y/cm	0	19	36	51	64	75	…

2024年广东省中考数学全真模拟试卷(一)

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

二、填空题：本大题共5小题，每小题3分，共15分．

三、解答题(一)：本大题共3小题，第16题10分，第17、18题各7分，共24分．

四、解答题(二)：本大题共3小题，每小题9分，共27分．

五、解答题(三)：本大题共2小题，每小题12分，共24分．

相关试卷 收起∨

相关试卷收起∨