2024年江苏省连云港市中考数学仿真模拟卷

修改时间：2024-05-11 浏览次数：84 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题（本大题共有8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）

1. 2023的相反数是（）

A . $\text{[math]}$ B . 2023 C . $\text{[math]}$ D . -2023

查看解析收藏纠错

+选题
2. 节能环保，从点滴做起！下面是节能环保的图片，图片上有图案和文字说明，其中图案是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 如图，甲是由一条直径、一条弦及一段圆弧所围成的图形；乙是由两条半径与一段圆弧所围成的图形；丙是由不过圆心 $\text{[math]}$ 的两条线段与一段圆弧所围成的图形.下列叙述正确的是（）

A . 只有甲是扇形 B . 只有乙是扇形 C . 只有丙是扇形 D . 只有乙、丙是扇形

查看解析收藏纠错

+选题
4. 可燃冰，学名叫“天然气水合物”，是一种高效清洁、储量巨大的新能源．据报道，仅我国可燃冰预测远景资源量就超过了1000亿吨油当量．将1000亿用科学记数法可表示为（）

A . 1×10³ B . 1000×10⁸ C . 1×10¹¹ D . 1×10¹⁴

查看解析收藏纠错

+选题
5. 如图，图1是一个底面为正方形的直棱柱；现将图1切割成图2的几何体，则图2的俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）.小亮同学随机地在大正方形及其内部区域投针，若直角三角形的两条直角边的长分别是2和1，则针扎到小正方形（阴影）区域的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 某校教师举行茶话会.若每桌坐10人，则空出一张桌子；若每桌坐8人，还有6人不能就坐.设该校准备的桌子数为 $\text{[math]}$ ，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，正方形ABCD的边长为 $\text{[math]}$ ，直线EF经过正方形的中心O，并能绕着O转动，分别交AB、CD边于E、F点，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题（本大题共8小题，每小题3分，共24分.不需要写出解答过程，请把答案直接填写在答题卡相应位置上）

9.
计算：．

查看解析收藏纠错

+选题
10. 如图，数轴上的点P表示的数是﹣1，将点P向右移动3个单位长度得到点P′，则点P′表示的数是．

查看解析收藏纠错

+选题
11. 一个三角形三条边长分别为xcm、（x+1）cm、（x+2）cm，它的周长不超过39cm，则x的取值范围是．

查看解析收藏纠错

+选题
12. 若关于x的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则m的值为．

查看解析收藏纠错

+选题
13. 在平面直角坐标系中，O为坐标原点，点A(-a，a)(a>0)，点B(-a-4，a+3)，C为该直角坐标系内的一点，连结AB，OC．若AB／／OC且AB=OC，则点C的坐标为

查看解析收藏纠错

+选题
14. 如图，在△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，其中点B的运动路径为 $\text{[math]}$ ，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
15. 如图，点A、点B是双曲线y＝ $\text{[math]}$ 上的两点，OA＝OB＝6，sin∠AOB＝ $\text{[math]}$ ，则k＝.

查看解析收藏纠错

+选题
16. 如图，在△ABC中，BC=6，BC边上的高为4，在△ABC的内部作一个矩形EFGD，使EF在BC边上，另外两个顶点分别在AB、AC边上，则对角线EG长的最小值为．

查看解析收藏纠错

+选题

三、解答题（本大题共11小题，共102分.请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤，作图过程需保留作图痕迹）

17. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 解方程组： $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 解方程： $\text{[math]}$

查看解析收藏纠错

+选题
20.
如图，菱形ABCD中，DE⊥AB于E，DF⊥BC于F．
（1）求证：△ADE≌△CDF；
（2）若∠EDF=50°，求∠BEF的度数．

查看解析收藏纠错

+选题
21. 某校举办以2022年北京冬奥会为主题的知识竞赛，从七年级和八年级各随机抽取了50名学生的竞赛成绩进行整理、描述和分析，部分信息如下：
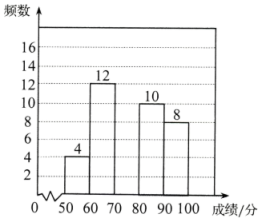
a：七年级抽取成绩的频数分布直方图如图．（数据分成5组， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

b：七年级抽取成绩在7 $\text{[math]}$ 这一组的是：70，72，73，73，75，75，75，76，77，77，78，78，79，79，79，79．

c：七、八年级抽取成绩的平均数、中位数如下：

年级

平均数

中位数

七年级

76.5

m

八年级

78.2

79

请结合以上信息完成下列问题：

（1）七年级抽取成绩在 $\text{[math]}$ 的人数是，并补全频数分布直方图；

（2）表中m的值为；

（3）七年级学生甲和八年级学生乙的竞赛成绩都是78，则（填“甲”或“乙”）的成绩在本年级抽取成绩中排名更靠前；

（4）七年级的学生共有400人，请你估计七年级竞赛成绩90分及以上的学生人数．

查看解析收藏纠错

+选题
22. 在某次化学实验中，晓欢在实验桌上放置了1杯纯净水，1杯生理盐水，2杯白糖水，共4杯液体．装这些液体的烧杯相同且液体体积也相同（外观均相同），由于没有贴标签，所以最终晓欢也无法分辨烧杯中的液体具体是哪种．现在晓欢要对这些液体进行甄别．

（1）求从这4杯液体中任取1杯是生理盐水的概率；

（2）晓欢从这4杯液体中同时任取2杯，请用画树状图或列表法求晓欢取出的2杯均是白糖水的概率．

查看解析收藏纠错

+选题
23. 北京冬奥会期间，首钢滑雪大跳台因其“玉如意”的绝美造型，高水平赛道的精修和维护工作受到了各国参赛运动员的盛赞．下图是一条滑雪赛道的简化示意图，它主要由跳台、助滑道和着陆坡三部分组成，已知点B与点C间的高度差为32米，着陆坡CD的倾斜角 $\text{[math]}$ 为37°，参赛运动员们将从点D处出发，乘车沿水平方向行驶至点E处，再沿斜坡EF行驶26米至点F处，最后乘坐垂直于水平方向的电梯到达点A处．已知斜坡EF的坡比为1：2.4，电梯AF的高度为50米，求着陆坡CD的长度，（结果精确到1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
24. （概念认识）
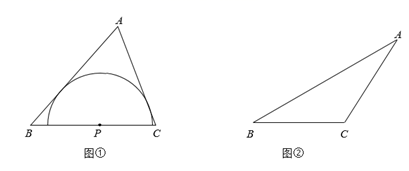
若以三角形某边上任意一点为圆心，所作的半圆上的所有点都在该三角形的内部或边上，则将符合条件且半径最大的半圆称为该边关联的极限内半圆.

如图①，点P是锐角△ABC的边BC上一点，以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时，半圆P为边BC关联的极限内半圆.

（1）（初步思考）若等边△ABC的边长为1，则边BC关联的极限内半圆的半径长为.

（2）如图②，在钝角△ABC中，用直尺和圆规作出边BC关联的极限内半圆（保留作图痕迹，不写作法）.

（3）（深入研究）如图③，∠AOB＝30°，点C在射线OB上，OC＝6，点Q是射线OA上一动点.在△QOC中，若边OC关联的极限内半圆的半径为r，当1≤r≤2时，求OQ的长的取值范围.

查看解析收藏纠错

+选题
25. 某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香，绿色健康”享誉全国，深受广大消费者喜爱．已知2件豆笋和3件豆干进货价为240元，3件豆笋和4件豆干进货价为340元．

（1）分别求出每件豆笋、豆干的进价；

（2）某特产店计划用不超过 $\text{[math]}$ 元购进豆笋、豆干共 $\text{[math]}$ 件，且豆笋的数量不低于豆干数量的 $\text{[math]}$ ，该特产店有哪几种进货方案？

（3）若该特产店每件豆笋售价为80元，每件豆干售价为55元，在（2）的条件下，怎样进货可使该特产店获得利润最大，最大利润为多少元？

查看解析收藏纠错

+选题
26. 在平面直角坐标系中，已知抛物线 $\text{[math]}$ .

（1）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“方点”.试求拋物线 $\text{[math]}$ 的“方点”的坐标；

（2）如图，若将该抛物线向左平移1个单位长度，新抛物线与 $\text{[math]}$ 轴相交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（ $\text{[math]}$ 在 $\text{[math]}$ 左侧），与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ .若点 $\text{[math]}$ 是直线 $\text{[math]}$ 上方抛物线上的一点，求 $\text{[math]}$ 的面积的最大值；

（3）第（2）问中平移后的抛物线上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 是以 $\text{[math]}$ 为直角边的直角三角形？若存在，直接写出所有符合条件的点 $\text{[math]}$ 的坐标；若不存在，说明理由.

查看解析收藏纠错

+选题
27. 如图甲，在△ABC中，∠ACB＝90°，AC＝4，BC＝3，动点P从点B出发，沿BA方向向点A匀速运动，同时动点Q从点A出发，沿AC方向向点C匀速运动，它们的速度均为1个单位/s，连接PQ ．设运动时间为t（s）（0＜t＜4），解答下列问题：

（1）设△APQ的面积为S ，则S＝；（用含t的代数式表示）

（2）如图乙，连接PC ，将△PQC沿QC翻折，得到四边形PQP’C ，当四边形PQP’C为菱形时，求t的值；

（3）当△APQ是等腰三角形时，求t的值？

查看解析收藏纠错

+选题

年级	平均数	中位数
七年级	76.5	m
八年级	78.2	79

2024年江苏省连云港市中考数学仿真模拟卷

一、选择题（本大题共有8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）

二、填空题（本大题共8小题，每小题3分，共24分.不需要写出解答过程，请把答案直接填写在答题卡相应位置上）

三、解答题（本大题共11小题，共102分.请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤，作图过程需保留作图痕迹）

相关试卷 收起∨

相关试卷收起∨