浙江省衢州市2023年中考数学试卷

1. 手机信号的强弱通常采用负数来表示，绝对值越小表示信号越强(午位： $\text{[math]}$ )，则下列信号最强的是（）

A . -50 B . -60 C . -70 D . -80

查看解析收藏纠错

+选题
2. 如图是国家级非物质文化遗产衢州莹白瓷的直口杯，它的主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算，结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 某公司5名员工在一次义务募捐中的捐款额为(单位：元)：30，50，50，60，60.若捐款最少的员工又多捐了20元，则分析这5名员工捐款额的数据时，不受影响的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

查看解析收藏纠错

+选题
5. 下列各组数满足方程 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图是脊柱侧弯的检测示意图，在体检时为方便测出Cobb角 $\text{[math]}$ 的大小，需将 $\text{[math]}$ 转化为与它相等的角，则图中与 $\text{[math]}$ 相等的角是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在△ABC中，以点A为圆心，适当长为半径画弧，分别交AB，AC于点D，E.分别以点D，E为圆心，大于 $\text{[math]}$ 长为半径画弧，交于∠BAC内一点F.连结AF并延长，交BC于点G，连结DG，EG.添加下列条件，不能使BG=CG成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 某人患了流感，经过两轮传染后共有36人患了流感.设每一轮传染中平均每人传染了 $\text{[math]}$ 人，则可得到方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，一款可调节的笔记本电脑支架放置在水平桌面上，调节杆 $\text{[math]}$ 的最大仰角为 $\text{[math]}$ .当 $\text{[math]}$ 时，则点 $\text{[math]}$ 到桌面的最大高度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 已知二次函数 $\text{[math]}$ 是常数， $\text{[math]}$ 的图象上有 $\text{[math]}$ 和 $\text{[math]}$ 两点.若点A，B都在直线 $\text{[math]}$ 的上方，且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都，如果他们可以选择其中任一航班，则他们选择同一航班的概率等于.

查看解析收藏纠错

+选题
13. 在如图所示的方格纸上建立适当的平面直角坐标系，若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为.

查看解析收藏纠错

+选题
14. 如图是一个圆形餐盘的正面及其固定支架的截面图，凹槽ABCD是矩形.当䝳盘正立且紧靠支架于点A，D时，恰好与BC边相切，则此餐盘的半径等于 $\text{[math]}$ .

查看解析收藏纠错

+选题
15. 如图，点A，B在 $\text{[math]}$ 轴上，分别以OA，AB为边，在 $\text{[math]}$ 轴上方作正方形OACD，ABEF.反比例函数 $\text{[math]}$ 的图象分别交边CD，BE于点P，Q.作 $\text{[math]}$ 轴于点 $\text{[math]}$ 轴于点 $\text{[math]}$ .若 $\text{[math]}$ 为BE的中点，且阴影部分面积等于6，则 $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
16. 下面是勾股定理的一种证明方法：图1所示纸片中， $\text{[math]}$ ，四边形ACDE，CBFG是正方形.过点C，B将纸片CBFG分别沿与AB平行、垂直两个方向剪裁成四部分，并与正方形 $\text{[math]}$ 拼成图2.

（1）若 $\text{[math]}$ 的面积为16，则纸片Ⅲ的面积为.

（2）若 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题

17.

（1）计算： $\text{[math]}$ .

（2）化简： $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 小红在解方程 $\text{[math]}$ 时，第一步出现了错误：

（1）请在相应的方框内用横线划出小红的错误处.

（2）写出你的解答过程.

查看解析收藏纠错

+选题
19. 已知：如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ 在同一条直线上.下面四个条件：
① $\text{[math]}$ ② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$

（1）请选择其中的三个条件，使得△ABC≌△DEF(写出一种情况即可).

（2）在(1)的条件下，求证：△ABC≌△DEF.

查看解析收藏纠错

+选题
20. 【数据的收集与整理】
根据国家统计局统一部署﹐衢州市统计局对2022年我市人口变动情况进行了抽样调查，抽样比例为5‰.根据抽样结果推算，我市2022年的出生率为5.5‰，死亡率为8‰，人口自然增长率为-2.5‰，常住人口数为 $\text{[math]}$ 人(‰来示千分号).

(数据来源：衢州市统计局)【数据分析】

（1）请根据信息推测人口自然增长率与出生率、死亡率的关系.

（2）已知本次调查的样本容量为11450，请推算 $\text{[math]}$ 的值.

（3）将我市及全国近五年的人口自然增长率情况绘制成如下统计图.根据统计图分析：

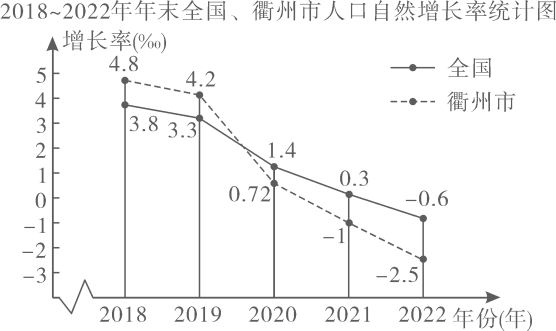
①对图中信息作出评判(写出两条).

②为扭转目前人口自然增长率的趋势，请给出一条合理化建议.

查看解析收藏纠错

+选题
21. 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ 为AC边上一点，连结OB.以OC为半径的半圆与AB边相切于点 $\text{[math]}$ ，交AC边于点 $\text{[math]}$ .

（1）求证： $\text{[math]}$ .

（2）若 $\text{[math]}$ .
①求半圆 $\text{[math]}$ 的半径.

②求图中阴影部分的面积.

查看解析收藏纠错

+选题

22. 视力表中蕴含着很多数学知识，如：每个“

”形图都是正方形结构，同一行的“

”是全等图形且对应着同一个视力值，不同的检测距离需要不同的视力表.

素材1国际通用的视力表以5米为检测距离，任选视力表中7个视力值 $\text{[math]}$ ，测得对应行的“”形图边长 $\text{[math]}$ ，在平面直角坐标系中描点如图1.

探究1检测距离为5米时，归纳 $\text{[math]}$ 与 $\text{[math]}$ 的关系式，并求视力值1.2所对应行的“”形图边长.

素材2图2为视网膜成像示意图，在检测视力时，眼晴能看清最小“”形图所成的角叫做分辨视角 $\text{[math]}$ .视力值 $\text{[math]}$ 与分辨视角 $\text{[math]}$ (分)的对应关系近似满足 $\text{[math]}$ ).

探究2当 $\text{[math]}$ 时，属于正常视力，根据函数增减性写出对应的分辦视角 $\text{[math]}$ 的范围.

素材3如图3，当 $\text{[math]}$ 确定时，在 $\text{[math]}$ 处用边长为 $\text{[math]}$ 的 $\text{[math]}$ 号“”测得的视力与在 $\text{[math]}$ 处用边长为 $\text{[math]}$ 的Ⅱ号“”测得的视力相同.

探究3若检测距离为3米，求视力值1.2所对应行的“”形图边长.

查看解析收藏纠错

+选题

23. 某龙舟队进行500米直道训练，全程分为启航，途中和冲刺三个阶段.图1，图2分别表示启航阶段和途中阶段龙舟划行总路程 $\text{[math]}$ 与时间 $\text{[math]}$ 的近似函数图象.启航阶段的函数表达式为 $\text{[math]}$ ；途中阶段匀速划行，函数图象为线段；在冲刺阶段，龙舟先加速后匀速划行，加速期龙舟划行总路程 $\text{[math]}$ 与时间 $\text{[math]}$ 的函数表达式为 $\text{[math]}$ .

（1）求出启航阶段 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式(写出自变量的取值范围).

（2）已知途中阶段龙舟速度为 $\text{[math]}$ .
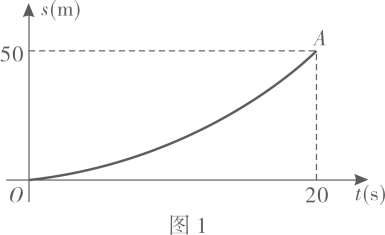
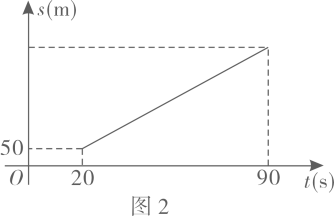
①当 $\text{[math]}$ 时，求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点，龙舟到达时， $\text{[math]}$ 视为达标.请说明该龙舟队能否达标.

（3）冲刺阶段，加速期龙舟用时 $\text{[math]}$ 将速度从 $\text{[math]}$ 提高到 $\text{[math]}$ ，之后保持匀速划行至终点.求该龙舟以完成训练所需时间(精确到 $\text{[math]}$ ).

查看解析收藏纠错

+选题
24. 如图1，点 $\text{[math]}$ 为矩形ABCD的对称中心， $\text{[math]}$ ，点 $\text{[math]}$ 为AD边上一点 $\text{[math]}$ ，连结EO并延长，交BC于点 $\text{[math]}$ .四边形ABFE与 $\text{[math]}$ 关于EF所在直线成轴对称，线段 $\text{[math]}$ 交AD边于点 $\text{[math]}$ 。

（1）求证： $\text{[math]}$ .

（2）当 $\text{[math]}$ 时，求AE的长.

（3）令AE=a，DG=b.
①求证：(4-a)(4-b)=4.

②如图2，连结 $\text{[math]}$ ，分别交 $\text{[math]}$ 于点H，K.记四边形OKGH的面积为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ .当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题

浙江省衢州市2023年中考数学试卷

一、选择题(本题共有10小题,每小题3分,共30分)

二、填空题(本题共有6小题,每小题4分,共24分)

三、解答题(本题共有8小题,第 rId164 小题每小题6分,第 rId166 小题每小题8分,第 rId168 23小题每小题10分,第24小题12分,共66分.请务必写出解答过程

相关试卷收起∨

浙江省衢州市2023年中考数学试卷

一、选择题(本题共有10小题,每小题3分,共30分)

二、填空题(本题共有6小题,每小题4分,共24分)

三、解答题(本题共有8小题,第 rId164 小题每小题6分,第 rId166 小题每小题8分,第 rId168 23小题每小题10分,第24小题12分,共66分.请务必写出解答过程

相关试卷 收起∨

相关试卷收起∨