江苏省淮安市2023年中考数学试卷

修改时间：2023-10-25 浏览次数：239 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列实数中，属于无理数的是（　　）

A . ﹣2 B . 0 C . $\text{[math]}$ D . 5

查看解析收藏纠错

+选题
2. 剪纸是中国优秀的传统文化．下列剪纸图案中，是轴对称图形的是（）．

A . B . C . D .

查看解析收藏纠错

+选题
3. 健康成年人的心脏每分钟流过的血液约 $\text{[math]}$ ．数据4900用科学记数法表示为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 下列计算正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 实数 $\text{[math]}$ 在数轴上的对应点的位置如图所示，下列结论正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 将直角三角板和直尺按照如图位置摆放，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图是一个几何体的三视图，则该几何体的侧面积是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象分别与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点，且与反比例函数 $\text{[math]}$ 在第一象限内的图象交于点 $\text{[math]}$ ．若点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

9. 若式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

查看解析收藏纠错

+选题
10. 方程 $\text{[math]}$ 的解是．

查看解析收藏纠错

+选题
11. 若等腰三角形的周长是 $\text{[math]}$ ，一腰长为 $\text{[math]}$ ，则这个三角形的底边长是 $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

查看解析收藏纠错

+选题
13. 将甲、乙两组各10个数据绘制成折线统计图(如图)，两组数据的平均数都是7，设甲、乙两组数据的方差分别为 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ (填“ $\text{[math]}$ ”“=”或“ $\text{[math]}$ ”)．

查看解析收藏纠错

+选题
14. 如图，四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接四边形， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是 $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 如图，3个大小完全相同的正六边形无缝隙、不重叠的拼在一起，连接正六边形的三个顶点得到 $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

查看解析收藏纠错

+选题
16. 在四边形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 内部的任一条射线（ $\text{[math]}$ 不等于 $\text{[math]}$ ），点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 面积的最大值是．

查看解析收藏纠错

+选题

三、解答题

17.

（1）计算： $\text{[math]}$ ；

（2）解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
18. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

查看解析收藏纠错

+选题
19. 已知：如图，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 小华、小玲一起到淮安西游乐园游玩，他们决定在三个热门项目（A：智取芭蕉扇、B：三打白骨精、C：盘丝洞）中各自随机选择一个项目游玩．

（1）小华选择C项目的概率是；

（2）用画树状图或列表等方法求小华、小玲选择不同游玩项目的概率．

查看解析收藏纠错

+选题

21. 为了调动员工的积极性，商场家电部经理决定确定一个适当的月销售目标，对完成目标的员工进行奖励．家电部对20名员工当月的销售额进行统计和分析．

数据收集（单位：万元）：

5.0 9.9 6.0 5.2 8.2 6.2 7.6 9.4 8.2 7.8

5.1 7.5 6.1 6.3 6.7 7.9 8.2 8.5 9.2 9.8

数据整理：

销售额/万元	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	3	5	$\text{[math]}$	4	4

数据分析：

平均数	众数	中位数
7.44	8	$\text{[math]}$

问题解决：

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ．

（2）若将月销售额不低于7万元确定为销售目标，则有名员工获得奖励．

（3）经理对数据分析以后，最终对一半的员工进行了奖励．员工甲找到经理说：“我这个月的销售额是7.5万元，比平均数7.44万元高，所以我的销售额超过一半员工，为什么我没拿到奖励？”假如你是经理，请你给出合理解释．

查看解析收藏纠错

+选题

22. 为了便于劳动课程的开展，学校打算建一个矩形生态园 $\text{[math]}$ （如图），生态园一面靠墙（墙足够长），另外三面用 $\text{[math]}$ 的篱笆围成．生态园的面积能否为 $\text{[math]}$ ？如果能，请求出 $\text{[math]}$ 的长；如果不能，请说明理由．

查看解析收藏纠错

+选题

23. 根据以下材料，完成项目任务，

项目	测量古塔的高度及古塔底面圆的半径
测量工具	测角仪、皮尺等
测量		说明：点 $\text{[math]}$ 为古塔底面圆圆心，测角仪高度 $\text{[math]}$ ，在 $\text{[math]}$ 处分别测得古塔顶端的仰角为 $\text{[math]}$ ，测角仪 $\text{[math]}$ 所在位置与古塔底部边缘距离 $\text{[math]}$ ．点 $\text{[math]}$ 在同一条直线上．
参考数据	$\text{[math]}$

项目任务

（1）求出古塔的高度．

（2）求出古塔底面圆的半径．

查看解析收藏纠错

+选题

24. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ．

（1）尺规作图：作 $\text{[math]}$ ，使得圆心 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ 过点 $\text{[math]}$ 且与边 $\text{[math]}$ 相切于点 $\text{[math]}$ （请保留作图痕迹，标明相应的字母，不写作法）；

（2）在（1）的条件下，若 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分的面积．

查看解析收藏纠错

+选题
25. 快车和慢车同时从甲地出发，以各自的速度匀速向乙地行驶，快车到达乙地卸装货物用时 $\text{[math]}$ ，结束后，立即按原路以另一速度匀速返回，直至与慢车相遇，已知慢车的速度为 $\text{[math]}$ ．两车之间的距离 $\text{[math]}$ 与慢车行驶的时间 $\text{[math]}$ 的函数图象如图所示．

（1）请解释图中点 $\text{[math]}$ 的实际意义；

（2）求出图中线段 $\text{[math]}$ 所表示的函数表达式；

（3）两车相遇后，如果快车以返回的速度继续向甲地行驶，求到达甲地还需多长时间．

查看解析收藏纠错

+选题
26. 已知二次函数 $\text{[math]}$ （ $\text{[math]}$ 为常数）．

（1）该函数图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点，若点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，
①则 $\text{[math]}$ 的值是 ▲ ，点 $\text{[math]}$ 的坐标是 ▲ ；
②当 $\text{[math]}$ 时，借助图像，求自变量 $\text{[math]}$ 的取值范围；

（2）对于一切实数 $\text{[math]}$ ，若函数值 $\text{[math]}$ 总成立，求 $\text{[math]}$ 的取值范围（用含 $\text{[math]}$ 的式子表示）；

（3）当 $\text{[math]}$ 时（其中 $\text{[math]}$ 为实数， $\text{[math]}$ ），自变量 $\text{[math]}$ 的取值范围是 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的值以及 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
27. 综合与实践
定义：将宽与长的比值为 $\text{[math]}$ （ $\text{[math]}$ 为正整数）的矩形称为 $\text{[math]}$ 阶奇妙矩形．

（1）概念理解：
当 $\text{[math]}$ 时，这个矩形为1阶奇妙矩形，如图（1），这就是我们学习过的黄金矩形，它的宽（ $\text{[math]}$ ）与长 $\text{[math]}$ 的比值是．

（2）操作验证：
用正方形纸片 $\text{[math]}$ 进行如下操作（如图（2））：
第一步：对折正方形纸片，展开，折痕为 $\text{[math]}$ ，连接 $\text{[math]}$ ；
第二步：折叠纸片使 $\text{[math]}$ 落在 $\text{[math]}$ 上，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ ，展开，折痕为 $\text{[math]}$ ；
第三步：过点 $\text{[math]}$ 折叠纸片，使得点 $\text{[math]}$ 分别落在边 $\text{[math]}$ 上，展开，折痕为 $\text{[math]}$ ．
试说明：矩形 $\text{[math]}$ 是1阶奇妙矩形．

（3）方法迁移：
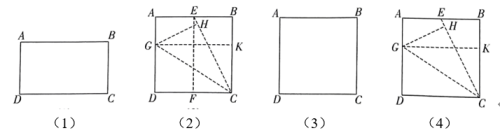
用正方形纸片 $\text{[math]}$ 折叠出一个2阶奇妙矩形．要求：在图（3）中画出折叠示意图并作简要标注．

（4）探究发现：
小明操作发现任一个 $\text{[math]}$ 阶奇妙矩形都可以通过折纸得到．他还发现：如图（4），点 $\text{[math]}$ 为正方形 $\text{[math]}$ 边 $\text{[math]}$ 上（不与端点重合）任意一点，连接 $\text{[math]}$ ，继续（2）中操作的第二步、第三步，四边形 $\text{[math]}$ 的周长与矩形 $\text{[math]}$ 的周长比值总是定值．请写出这个定值，并说明理由．

查看解析收藏纠错

+选题

江苏省淮安市2023年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨